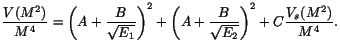

Next: Conclusion
Up: report
Previous: The energy resolution
In order to include the spatial corrections to the mass resolution we
recorded the mean of the
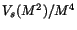 distributions for each (
distributions for each (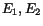 )
bin for both the
)
bin for both the  and
and  samples. Then we modified the expression
for the variance function (Eq. (3)), using Eq. (4) for
the contribution from energy resolution,
samples. Then we modified the expression
for the variance function (Eq. (3)), using Eq. (4) for
the contribution from energy resolution,
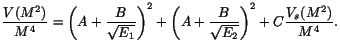 |
(10) |
In addition to the standard parameters 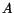 and
and 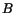 , we introduced parameter
, we introduced parameter
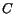 that scales the spatial resolution contribution. With this simple model
we first fitted
that scales the spatial resolution contribution. With this simple model
we first fitted  data with
data with  set to zero. The fit is shown as the
solid line in Fig. 8, while the fit parameters are shown in the
first row of Table 2. Next we let
set to zero. The fit is shown as the
solid line in Fig. 8, while the fit parameters are shown in the
first row of Table 2. Next we let  vary. The corresponding fit
is represented by the dashed line in Fig. 8 and the second row in
Table 2. The fit confirms that the
vary. The corresponding fit
is represented by the dashed line in Fig. 8 and the second row in
Table 2. The fit confirms that the  mass is not very sensitive
to spatial corrections. In the next step we fitted all measured points from
the
mass is not very sensitive
to spatial corrections. In the next step we fitted all measured points from
the  and
and  samples together. The fit is shown as the dotted line
in Fig. 8, and the resulting parameters are shown in the last row of
Table 2. Both the
samples together. The fit is shown as the dotted line
in Fig. 8, and the resulting parameters are shown in the last row of
Table 2. Both the  and
and  mass distributions are
described well by the model.
We used a single parameter to scale the spatial contribution to the mass
resolution. The energy-dependent part of the spatial error in Eq. (7)
is dominant at small and moderate angles
mass distributions are
described well by the model.
We used a single parameter to scale the spatial contribution to the mass
resolution. The energy-dependent part of the spatial error in Eq. (7)
is dominant at small and moderate angles
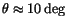 , while the
angular part in Eq. (7) becomes more important at large angles
, while the
angular part in Eq. (7) becomes more important at large angles
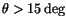 . We checked the importance of the angle-dependent spatial
errors by setting
. We checked the importance of the angle-dependent spatial
errors by setting 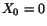 in Eq. (7), which made the overall
in Eq. (7), which made the overall
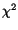 worse. We conclude that it is important to use elliptically errors
at larger angles. The scale parameter
worse. We conclude that it is important to use elliptically errors
at larger angles. The scale parameter 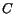 can be viewed as a correction to
the nominal value of
can be viewed as a correction to
the nominal value of 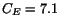 mm
mm GeV
GeV
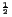 for the LGD.
for the LGD.
Table 2:
The parameter values from different fits to the  and
and  mass resolutions, obtained using Eq. (10). The corresponding
fits are shown in Fig. 8
mass resolutions, obtained using Eq. (10). The corresponding
fits are shown in Fig. 8
| Fit |
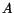 |
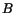
![$ \left[GeV^{-1/2}\right]$](img92.png) |
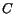 |
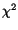 |
 ( (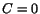 ) ) |
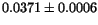 |
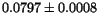 |
0 |
1.05 |
 (full) (full) |
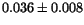 |
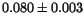 |
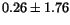 |
1.04 |
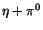 (full) (full) |
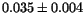 |
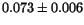 |
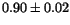 |
1.50 |
Figure 3:
Energy distribution of 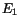 vs.
vs. 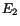 (red boxes). Green dots represent
showers with invariant mass close to the
(red boxes). Green dots represent
showers with invariant mass close to the  mass (right) and
mass (right) and  mass (left). Black dots represent the pairs of photon energies for which
mass (left). Black dots represent the pairs of photon energies for which
 has been fitted. Solid lines correspond to the case when
has been fitted. Solid lines correspond to the case when  .
.
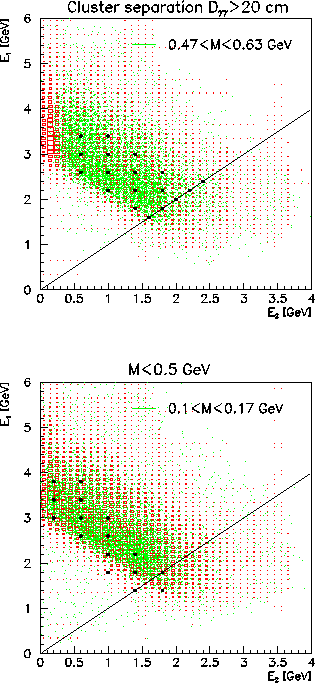 |
Figure 4:
The  squared-mass distributions for 9 energy bins, fitted with a
Gaussian. The dotted lines represent a polynomial background. Below each
plot are shown the corresponding energies (
squared-mass distributions for 9 energy bins, fitted with a
Gaussian. The dotted lines represent a polynomial background. Below each
plot are shown the corresponding energies (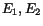 ).
).
 |
Figure 5:
The same as Fig. 4 for energy bins 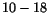 .
.
 |
Figure 6:
The  mass distribution for 8 energy bins, fitted with a Gaussian.
The dotted lines represent a polynomial background.
mass distribution for 8 energy bins, fitted with a Gaussian.
The dotted lines represent a polynomial background.
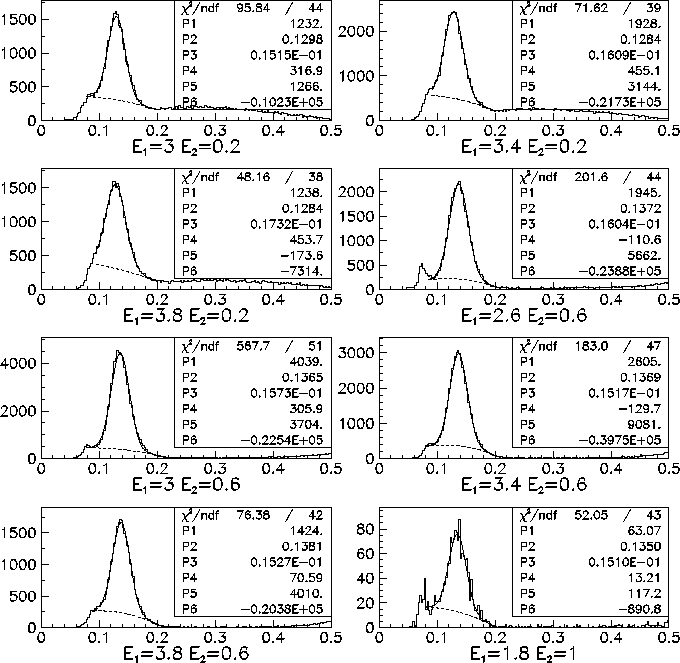 |
Figure 7:
The same as Fig. 6 for energy bins  .
.
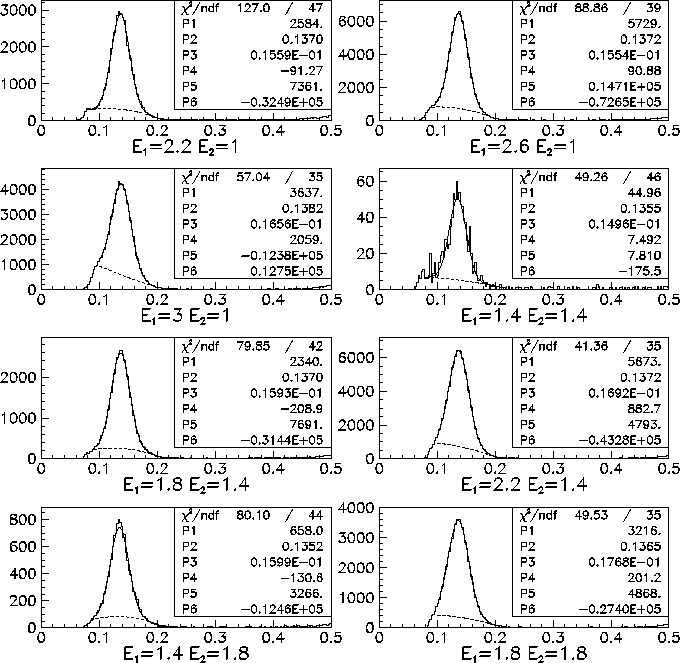 |
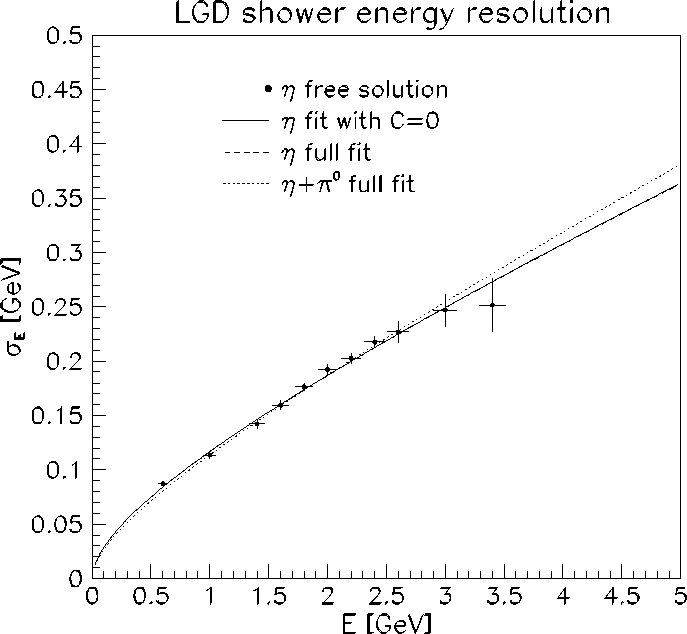
Figure 8:
Energy resolution of showers in the LGD obtained from analysis of the
 sample. Points represent the free solution to the
sample. Points represent the free solution to the  squared-mass resolution measurements when the contribution from the spatial
resolution has been neglected. The solid line represents the fit to the
squared-mass resolution measurements when the contribution from the spatial
resolution has been neglected. The solid line represents the fit to the  data with the standard energy resolution model (Eq. (10)with
data with the standard energy resolution model (Eq. (10)with 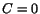 ).
The dashed line represents the fit to the
).
The dashed line represents the fit to the  data when the spatial
contribution is taken into account by Eq. (10). The dotted line
corresponds to the simultaneous fit to the
data when the spatial
contribution is taken into account by Eq. (10). The dotted line
corresponds to the simultaneous fit to the  and
and  data with the
same function (Eq. (10)). Corresponding fit parameters and
data with the
same function (Eq. (10)). Corresponding fit parameters and 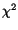 are shown in Table 2.
are shown in Table 2.
 |


Next: Conclusion
Up: report
Previous: The energy resolution
Richard T. Jones
2003-10-04