

Next: Bibliography
Up: report
Previous: Spatial corrections
We analyzed the invariant mass distributions from
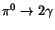 and
and
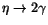 decays to extract the single shower energy and position
resolution. To a good approximation, the width of the
decays to extract the single shower energy and position
resolution. To a good approximation, the width of the  mass peak is
mainly determined by the energy resolution, while the
mass peak is
mainly determined by the energy resolution, while the  mass is heavily
affected by the spatial resolution. This feature is related to the fact that
the detector is close to the target and
mass is heavily
affected by the spatial resolution. This feature is related to the fact that
the detector is close to the target and  shower pairs from have
separations close to the detector acceptance.
In the first approximation we neglected the spatial contribution to the
shower pairs from have
separations close to the detector acceptance.
In the first approximation we neglected the spatial contribution to the  mass resolution and measured the squared-mass variance for a set of
well-defined shower energies (
mass resolution and measured the squared-mass variance for a set of
well-defined shower energies (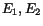 ).
From this measurement we a obtained model-independent solution to the energy
resolution function. This solution is in good agreement with the standard
expression used to describe the energy resolution of lead glass. In order to
incorporate the
).
From this measurement we a obtained model-independent solution to the energy
resolution function. This solution is in good agreement with the standard
expression used to describe the energy resolution of lead glass. In order to
incorporate the  data into the same description, we introduced a
standard expression for the shower centroid resolution. The spatial
contribution to the mass resolution is scaled by a free parameter
data into the same description, we introduced a
standard expression for the shower centroid resolution. The spatial
contribution to the mass resolution is scaled by a free parameter 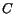 .
The
.
The  data showed no sensitivity to the value of the parameter
data showed no sensitivity to the value of the parameter  .
In order to fix the set of parameters that governs the LGD resolution, we
performed a simultaneous fit to 34
.
In order to fix the set of parameters that governs the LGD resolution, we
performed a simultaneous fit to 34  and
and  mass resolution
measurements. From the fit, we obtained for the energy resolution function
mass resolution
measurements. From the fit, we obtained for the energy resolution function
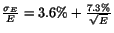
,
and for the shower position uncertainty
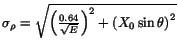
,
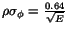
,
where (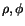 ) are the polar coordinates of the shower in the face of
the LGD. All lengths in these relations are in mm and all energies in GeV.
The mass widths of both the
) are the polar coordinates of the shower in the face of
the LGD. All lengths in these relations are in mm and all energies in GeV.
The mass widths of both the  and
and  from
from 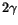 events
are explained very well with this single set of parameters.
events
are explained very well with this single set of parameters.


Next: Bibliography
Up: report
Previous: Spatial corrections
Richard T. Jones
2003-10-04
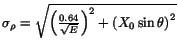 ,
,