

Next: Discussion
Up: psf
Previous: Introduction
There are various functions that have been used to describe the shape of
showers in EM calorimeters. Usually one uses a sum of 2 functions:
a core part that describes the peak of the energy distribution and a
second one that covers the tail. Among others, two exponential, exponential
and Gaussian, and two Gaussian functions have been exploited [2].
The single shower fitter is built to use an arbitrary PSF function without
changing the algorithm.
The first step in fitting an event is to get initial values for the fitting
parameters,
 , from the data. In the case of an isolated shower,
E is set to the total energy in the LGD,
, from the data. In the case of an isolated shower,
E is set to the total energy in the LGD, 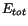 , while
, while 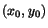 is set by the coordinates of the block with maximum energy yield.
The fit is performed using MINIUT. In order to speed up fitting, we decided not
to fit the whole LGD array, but rather a matrix (currently 9X9) around
the maximum energy block. The fitter minimizes
is set by the coordinates of the block with maximum energy yield.
The fit is performed using MINIUT. In order to speed up fitting, we decided not
to fit the whole LGD array, but rather a matrix (currently 9X9) around
the maximum energy block. The fitter minimizes 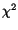
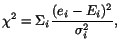 |
(1) |
where 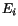 is the observed block energy, and
is the observed block energy, and 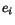 is the PSF function taken
at the center of the block. Errors
is the PSF function taken
at the center of the block. Errors 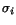 in Eq. 1 are calculated
from expression
in Eq. 1 are calculated
from expression
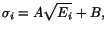 |
(2) |
with A=0.08 and B=0.01.
The first trial function to be used is a single Gaussian
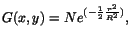 |
(3) |
with 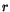 being the radial distance from the shower center
being the radial distance from the shower center
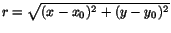 .
The normalization
.
The normalization 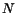 is determined by the the shower energy E,
N = E/(2
is determined by the the shower energy E,
N = E/(2 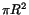 ). In order to get the proper overall normalization
one has to multiply Eq. 3 with the LGD block area
). In order to get the proper overall normalization
one has to multiply Eq. 3 with the LGD block area 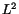 .
The radial Gaussian width
.
The radial Gaussian width 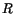 should be fixed, but can be a function
of energy E and angle
should be fixed, but can be a function
of energy E and angle 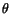 . In Fig. 1 is shown how R converges,
when it is used as a free parameter, to the value
. In Fig. 1 is shown how R converges,
when it is used as a free parameter, to the value
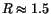 while
shower energy increases. For
while
shower energy increases. For 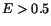 GeV,
GeV, 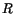 is almost independent
of energy. It seems this is a feature of MC showers, connected with the fact
that core contribution, consisting of just two central blocks,
is much more prominent than the tail. We will try to explain this later.
An additional result from the first fit is that the fitted energy is biased
by
is almost independent
of energy. It seems this is a feature of MC showers, connected with the fact
that core contribution, consisting of just two central blocks,
is much more prominent than the tail. We will try to explain this later.
An additional result from the first fit is that the fitted energy is biased
by
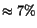 towards lower values with respect to the generated energy.
towards lower values with respect to the generated energy.
Figure 1:
Radial width 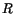 vs. energy for 0.1, 0.5, 1.0, 2.0, 3.0, 3.5
vs. energy for 0.1, 0.5, 1.0, 2.0, 3.0, 3.5 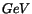 photons shot in the direction of
photons shot in the direction of
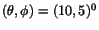 . Left:
initial
. Left:
initial 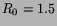 ,
, 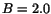 . Right: initial
. Right: initial 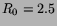 ,
, 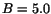 .
Note: when
.
Note: when  is allow to vary,
is allow to vary,  has to be large in order to
stabilize fitter and get physically acceptable fits.
has to be large in order to
stabilize fitter and get physically acceptable fits.
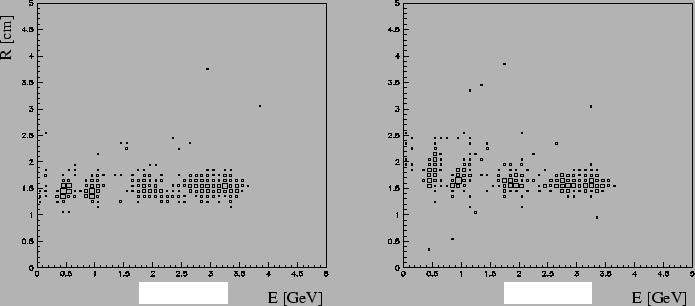 |
Figure 2:
Fit-data difference, averaged over 100 shots,
for 0.1, 1.0, and 3.5 GeV photons,
(top-left, top-right and bottom colored plot respectively).
Data are superimposed for comparison (black boxes).
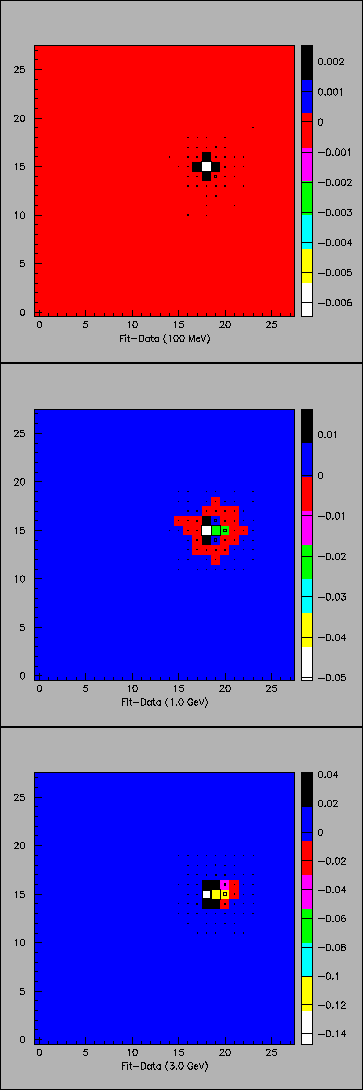 |
When 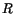 is fixed to its average value of 1.7, the negative energy bias in
the fitted energy increases to
is fixed to its average value of 1.7, the negative energy bias in
the fitted energy increases to
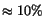 . Comparing data with function,
block by block (Fig. 2), it is found that the negative bias comes
from an under-estimate of the two central blocks.
There are two possible explanations: MC showers are not Gaussian, or
we are misinterpreting the "true" shape by sampling a function
at the center of the block.
The second consideration is based on the following observation:
for radial widths of order
. Comparing data with function,
block by block (Fig. 2), it is found that the negative bias comes
from an under-estimate of the two central blocks.
There are two possible explanations: MC showers are not Gaussian, or
we are misinterpreting the "true" shape by sampling a function
at the center of the block.
The second consideration is based on the following observation:
for radial widths of order
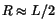 ,
a Gaussian is changing rapidly across the block.
While we sample the function at the center of the block, the actual function
value can be quite different at the block edges. It might be necessary to
integrate over a block to guess the shape of the PSF.
Proper normalization of the function requires multiplication with the block
area.
This is equivalent to 0-th order expansion of the integral
,
a Gaussian is changing rapidly across the block.
While we sample the function at the center of the block, the actual function
value can be quite different at the block edges. It might be necessary to
integrate over a block to guess the shape of the PSF.
Proper normalization of the function requires multiplication with the block
area.
This is equivalent to 0-th order expansion of the integral
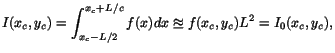 |
(4) |
around the center of the block  .
On the other hand, for any 2-dim function, a 2-nd order expansion can
be obtained from
.
On the other hand, for any 2-dim function, a 2-nd order expansion can
be obtained from
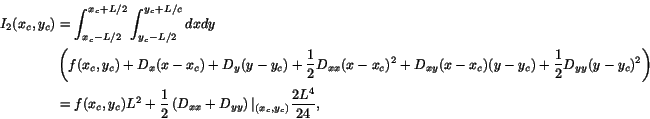 |
(5) |
where  stands for a partial derivative of
stands for a partial derivative of 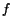 with respect to a particular
index. In the case of the Gaussian, this is reduced to
with respect to a particular
index. In the case of the Gaussian, this is reduced to
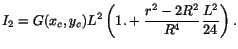 |
(6) |
The true value of the integral over the block area is given by
![$\displaystyle I = \frac{E}{2} \left[ erf\left( \frac{\Delta x-L/2}{\sqrt{2}R} \...
...qrt{2}R} \right)
- erf \left( \frac{\Delta y+L/2}{\sqrt{2}R} \right) \right],$](img45.png) |
(7) |
with
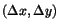 being
being
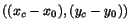 .
Table 1 shows a block-by-block comparison of data with
.
Table 1 shows a block-by-block comparison of data with
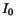 ,
, 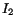 , and
, and 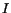 , from two showers with 1.0 GeV and 3.5 GeV photons.
For the first shower, the
, from two showers with 1.0 GeV and 3.5 GeV photons.
For the first shower, the 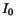 approximation is used as the PSF and the
radial width obtained is
approximation is used as the PSF and the
radial width obtained is
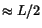 if
if 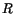 is allowed to vary.
One can see that
is allowed to vary.
One can see that 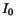 significantly differs from
significantly differs from 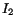 and
and 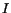 .
In the second case the integral
.
In the second case the integral 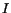 is used as the PSF, with
is used as the PSF, with
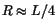 ,
where both
,
where both 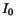 and
and 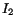 differ from
differ from 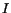 .
.
Table 1:
Comparison between 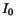 ,
, 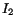 , and
, and 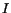 from two fits.
Note: not all blocks with non-zero data have been shown.
from two fits.
Note: not all blocks with non-zero data have been shown.
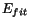 |
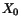 |
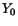 |
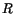 |
|
|
| 0.891053 |
19.606381 |
5.840514 |
1.607639 |
|
|
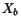 |
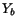 |
Data |
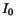 |
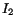 |
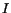 |
| 18.0 |
2.0 |
0.025080 |
0.030720 |
0.068005 |
0.065595 |
| 22.0 |
2.0 |
0.027360 |
0.016705 |
0.042231 |
0.044924 |
| 26.0 |
2.0 |
0.004560 |
0.000019 |
0.000112 |
0.000352 |
| 18.0 |
6.0 |
0.533520 |
0.530301 |
0.394643 |
0.408305 |
| 22.0 |
6.0 |
0.291840 |
0.288370 |
0.305232 |
0.279637 |
| 26.0 |
6.0 |
0.059280 |
0.000321 |
0.001467 |
0.002193 |
| 18.0 |
10.0 |
0.010260 |
0.018751 |
0.046285 |
0.046610 |
| 22.0 |
10.0 |
0.002280 |
0.010196 |
0.028374 |
0.031922 |
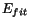 |
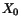 |
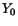 |
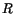 |
|
|
| 2.701281 |
21.084819 |
6.086944 |
0.966082 |
|
|
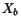 |
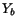 |
Data |
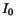 |
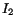 |
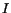 |
| 18.0 |
2.0 |
0.030780 |
0.000006 |
0.000115 |
0.005431 |
| 22.0 |
2.0 |
0.004560 |
0.000612 |
0.007948 |
0.036056 |
| 26.0 |
2.0 |
0.002280 |
0.000000 |
0.000000 |
0.000053 |
| 18.0 |
6.0 |
0.346560 |
0.044842 |
0.307623 |
0.339312 |
| 22.0 |
6.0 |
2.256060 |
4.686579 |
1.022599 |
2.252726 |
| 26.0 |
6.0 |
0.139080 |
0.000018 |
0.000317 |
0.003307 |
| 18.0 |
10.0 |
0.019380 |
0.000012 |
0.000229 |
0.008419 |
| 22.0 |
10.0 |
0.045600 |
0.001288 |
0.015373 |
0.055895 |
In Fig. 3
is shown the profile of the fitted energy as a function of
the generated energy obtained using 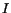 . The energy bias is essentially
unchanged, relative to the case where
. The energy bias is essentially
unchanged, relative to the case where 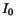 is used.
The radial width again weakly depends on energy but it drops to
is used.
The radial width again weakly depends on energy but it drops to
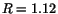 averaged over photon energies. Table 2 shows
the average fitted
averaged over photon energies. Table 2 shows
the average fitted 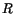 as a function of shower energy.
Figs. 4, 5, and 6 show a comparison between MC data
and the PSF (
as a function of shower energy.
Figs. 4, 5, and 6 show a comparison between MC data
and the PSF (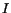 function), for
function), for 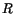 fixed to the values from Table 2.
Comparing fit-data differences for various shower energies
(bottom right plots on Fig. 4, 5, and 6)
with the similar ones obtained by
fixed to the values from Table 2.
Comparing fit-data differences for various shower energies
(bottom right plots on Fig. 4, 5, and 6)
with the similar ones obtained by 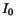 (Fig. 2) one can see
that central blocks are fitted better with
(Fig. 2) one can see
that central blocks are fitted better with 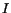 than with
than with 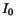 .
.
Table 2:
Average 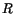 and energies, and corresponding errors,
for fits obtained by the
and energies, and corresponding errors,
for fits obtained by the 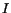 -function. Once
-function. Once 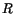 is fixed to the value
from the left-most column, average fitted energy again decreases
so that overall negative bias reappears.
is fixed to the value
from the left-most column, average fitted energy again decreases
so that overall negative bias reappears.
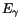 [ [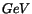 ] ] |
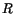 [ [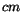 ] ] |
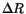 [ [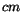 ] ] |
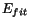 [ [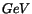 ] ] |
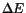 [ [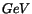 ] ] |
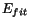 [ [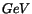 ](fixed ](fixed 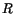 ) ) |
| 0.1 |
1.30 |
0.16 |
0.1 |
0.02 |
0.092 |
| 0.5 |
1.16 |
0.19 |
0.47 |
0.05 |
0.45 |
| 1.0 |
1.12 |
0.16 |
0.93 |
0.07 |
0.90 |
| 2.0 |
1.13 |
0.13 |
1.85 |
0.13 |
1.81 |
| 3.0 |
1.11 |
0.10 |
2.77 |
0.17 |
2.72 |
| 3.5 |
1.12 |
0.12 |
3.25 |
0.16 |
3.18 |
Figure:
The profile of the fitted energy as a function of the total energy
in the LGD, obtained using
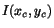 , and values of
, and values of  from the Table 2.
The straight dashed line represents unbiased fit.
from the Table 2.
The straight dashed line represents unbiased fit.
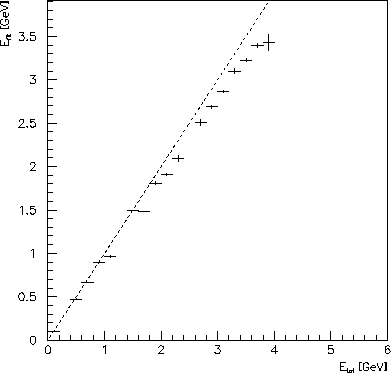 |
Figure 4:
Comparison of average data with
 and PSF
(top-left and top-right plots respectively), for fixed
and PSF
(top-left and top-right plots respectively), for fixed  ,
in the case of 0.1 GeV photons. Bottom-left plot represent errors,
while bottom-right shows fit-data difference. Box-plots are superimposed
for comparison.
,
in the case of 0.1 GeV photons. Bottom-left plot represent errors,
while bottom-right shows fit-data difference. Box-plots are superimposed
for comparison.
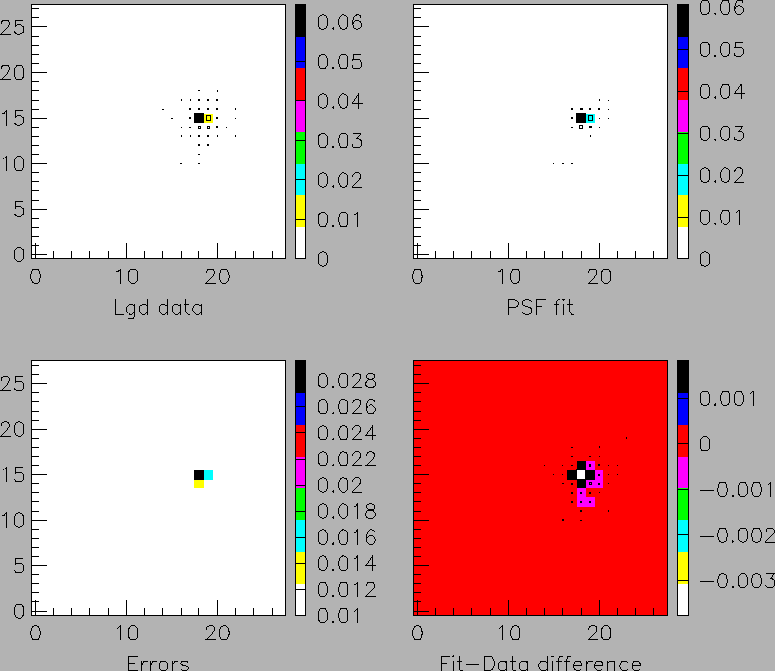 |
Figure 5:
The same as Fig. 4 for 1.0 GeV photons.
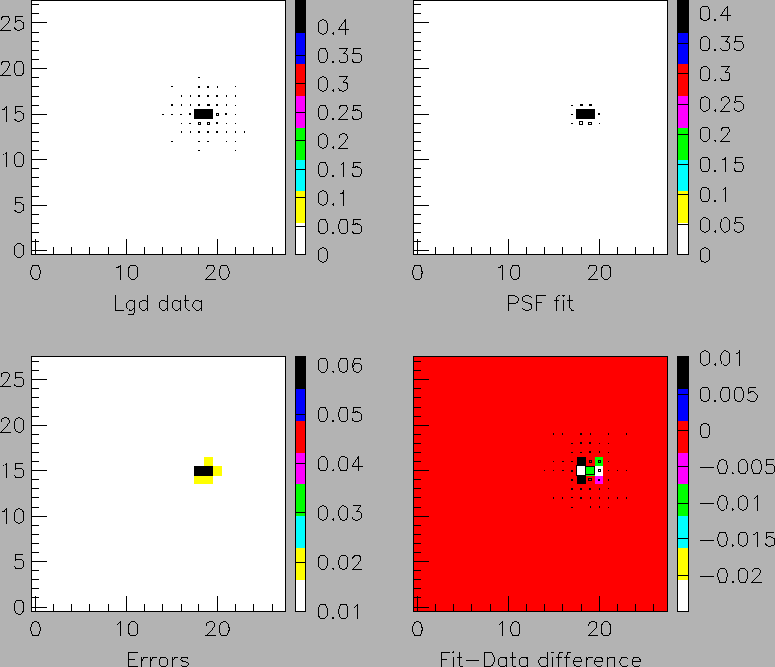 |
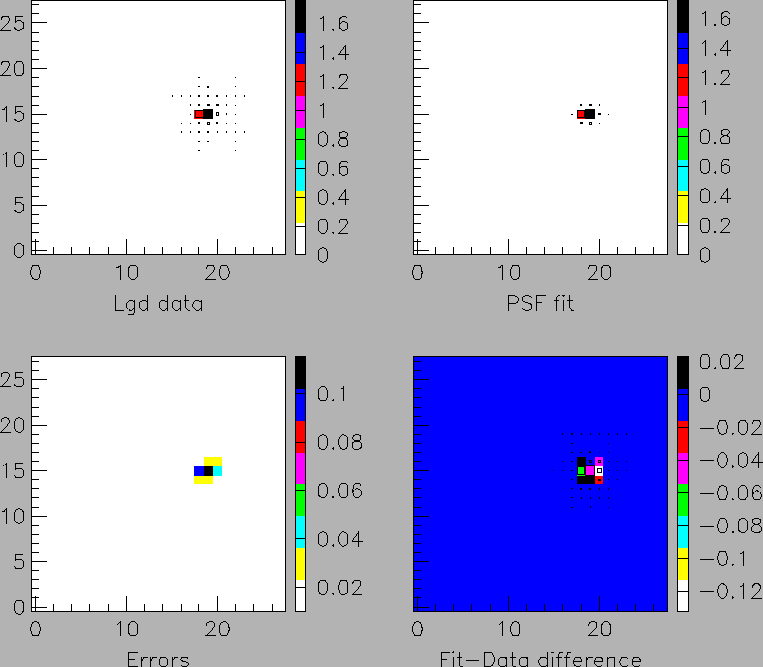
Figure 6:
The same as Fig. 4 for 3.5 GeV photons.
 |


Next: Discussion
Up: psf
Previous: Introduction
Richard T. Jones
2004-04-30



