Huygens Principle for a Planar Source

We start off with Maxwell's Equation in the Lorentz gauge:

$\square ^{2}A^{\mu }(\mathbf {r} ,t)=\square ^{2}A^{\mu }(r)=\mu j^{\mu }(r)$

where we use the metric signature (+,+,+,-) and

$A^{\mu }=(\mathbf {A} ,{\frac {\Phi }{c}})$

$\square ^{2}=\partial _{\mu }\partial ^{\mu }=\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}$

$j^{\mu }=(\mathbf {j} ,c\rho ),\partial _{\mu }=(\mathbf {\nabla } ,{\frac {1}{c}}{\frac {\partial }{\partial t}})$

The gauge condition for the Lorentz gauge is

$\partial _{\mu }A^{\mu }=0\Rightarrow \mathbf {\nabla } \cdot \mathbf {A} -{\frac {1}{c^{2}}}{\frac {\partial \Phi }{\partial t}}=0$

Introduce the Green's function at $r=(\mathbf {r} ,t)$ from some impulse source at $r'=(\mathbf {r} ',t')$

$\square _{r}^{2}G(r,r')=\delta ^{4}(r-r')$

and its Fourier transform

${\tilde {G}}(q)={\frac {1}{(2\pi )^{2}}}\int d^{4}r\,e^{-iq\cdot r}G(r,0)$

$G(r,0)={\frac {1}{(2\pi )^{2}}}\int d^{4}q\,e^{iq\cdot r}{\tilde {G}}(q)$

Translational symmetry implies

$G(r-r',0)=G(r,r')\quad$

so that

$G(r,r')={\frac {1}{(2\pi )^{2}}}\int d^{4}q\,e^{iq\cdot (r-r')}{\tilde {G}}(q)$

$\square _{r}^{2}G(r,r')={\frac {1}{(2\pi )^{2}}}\int d^{4}q\,(-q^{2})e^{iq\cdot (r-r')}{\tilde {G}}(q)$

$\square _{r}^{2}G(r,r')={\frac {1}{(2\pi )^{2}}}\int d^{4}q\,e^{iq\cdot (r-r')}(-k^{2}+{\frac {\omega ^{2}}{c^{2}}})$

where $q=(\mathbf {k} ,{\frac {\omega }{c}})$. But

$\square _{r}^{2}G(r,r')=\delta ^{4}(r-r')={\frac {1}{(2\pi )^{4}}}\int d^{4}q\,e^{iq\cdot (r-r')}$

${\tilde {G}}(q)={\frac {(2\pi )^{2}}{(2\pi )^{4}}}{\frac {1}{-q^{2}}}={\frac {-1}{(2\pi )^{2}q^{2}}}$

$G(r,r')={\frac {-1}{(2\pi )^{4}}}\int d^{4}q\,e^{iq\cdot (r-r')}{\frac {1}{(k+{\frac {\omega }{c}})(k-{\frac {\omega }{c}})}}$

Chose the "retarded" solution, such that the function is zero unless t>t'.

$G(r,r')={\frac {1}{(2\pi )^{4}}}\int d^{3}k\,e^{i\mathbf {k} \cdot (r-r')}\int d({\frac {\omega }{c}}){\frac {e^{-i\omega (t-t')}}{({\frac {\omega }{c}}-k)({\frac {\omega }{c}}+k)}}\Theta (t-t')$

$={\frac {1}{(2\pi )^{4}}}\int d^{3}k\,e^{i\mathbf {k} \cdot (r-r')}(2\pi i{\frac {e^{ick(t-t')}-e^{-ick(t-t')}}{2k}})\Theta$

$={\frac {-2\pi }{(2\pi )^{4}}}\int _{0}{\frac {k^{2}dk}{k}}\sin \left({ck(t-t')}\right)2\pi \int _{-1}^{1}dze^{ik|\mathbf {r} -\mathbf {r'} |z}\Theta$

$={\frac {-1}{(2\pi )^{2}}}\left({\frac {1}{|\mathbf {r} -\mathbf {r'|} }}\right)2\int _{0}dk\sin(ck(t-t'))\sin(k|\mathbf {r} -\mathbf {r'} |)\Theta$

$={\frac {1}{(2\pi )^{2}}}{\frac {2}{|\mathbf {r} -\mathbf {r} '|}}{\frac {2\pi }{4}}\left[\delta (|\mathbf {r} -\mathbf {r} '|+c(t-t'))-\delta (|\mathbf {r} -\mathbf {r} '|-c(t-t'))\right]\Theta$

But the term $\delta (|\mathbf {r} -\mathbf {r} '|+c(t-t'))\rightarrow 0\quad \forall \quad t>t'$ so that

$G(r,r')={\frac {-1}{4\pi }}\quad {\frac {\delta (|\mathbf {r} -\mathbf {r} '|-c(t-t'))}{|\mathbf {r} -\mathbf {r} '|}}$

Now to get the $G_{1}(r,r')\quad$ in the half-space with z>0 with the boundary condition $G_{1}\quad$ at$r_{3}=z=0\quad$   we take the difference:

$G_{1}(r,r')={\frac {-1}{4\pi }}\left({\frac {\delta (|\mathbf {r} -\mathbf {r} '|-c(t-t'))}{|\mathbf {r} -\mathbf {r} '|}}-{\frac {\delta (|\mathbf {r} -\mathbf {r} '+2z'{\hat {e_{3}}}|-c(t-t'))}{|\mathbf {r} -\mathbf {r} '+2z'{\hat {e_{3}}}|}}\right)$

Now use Green's theorem, with the generating function

$F^{\mu }=A(r)\partial _{\mu }G_{1}(r,r')-G_{1}(r,r')\partial _{\mu }A(r)$

$\int \partial _{\mu }F_{\mu }d^{4}r=\int cdt\int d^{3}r[\partial _{\mu }A\partial ^{\mu }G+A\partial _{\mu }\partial ^{\mu }G_{1}-\partial _{\mu }G\partial ^{\mu }A-G_{1}\partial _{\mu }\partial ^{\mu }A]$

$\partial _{\mu }\partial ^{\mu }G_{1}(r,r')=\delta ^{4}(r-r')$

$\partial _{\mu }\partial ^{\mu }A(r)=\mu j(r)$, let $j(r)=0\quad$

$\int \partial _{\mu }F_{\mu }d^{4}r=A(r')$

Now invoke the divergence theorem on the half space $z>0\quad$:

$A(r')=-\int d^{2}r\int cdt\left[A(r){\frac {\partial }{\partial z}}G_{1}(r,r')-G_{1}(r,r'){\frac {\partial }{\partial z}}A(r)\right]$, where the last term is zero by the condition of$G_{1}(z=0,r')=0\quad$

$A(r')=-c\int dt\int d^{2}rA(r){\frac {\partial }{\partial z}}G_{1}(r,r')$

To do the t integral, I need to bring out the z derivative. To do this, I first turn it into a z' derivative, using the relation

$G_{1}(r,r')={\frac {-1}{4\pi }}\left({\frac {\delta (|\mathbf {r} -\mathbf {r} '|-c(t-t'))}{|\mathbf {r} -\mathbf {r} '|}}-{\frac {\delta (|\mathbf {r} -\mathbf {r} ''|-c(t-t'))}{|\mathbf {r} -\mathbf {r} ''|}}\right)$

where $\mathbf {r} ''=\mathbf {r} '-2z'{\hat {e_{3}}}$

${\frac {\partial }{\partial z}}G_{1}(r,r')={\frac {-1}{4\pi }}\left({\frac {\partial }{\partial z}}\left({\frac {\delta (|\mathbf {r} -\mathbf {r} '|-c(t-t'))}{|\mathbf {r} -\mathbf {r} '|}}-{\frac {\delta (|\mathbf {r} -\mathbf {r} ''|-c(t-t'))}{|\mathbf {r} -\mathbf {r} ''|}}\right)\right)$

∴ $A(r')={\frac {-1}{4\pi }}{\frac {\partial }{\partial z'}}\int _{z=0}d^{2}r\left(2{\frac {A(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}})}{|\mathbf {r} -\mathbf {r} '|}}\right)$

At $z=0\quad$, $|\mathbf {r} -\mathbf {r} '|={\sqrt {r^{2}+z'^{2}}}=S,dS={\frac {rdr}{\sqrt {r^{2}+z'^{2}}}}$

If$A(\mathbf {r} ,t)\quad$ is independent of position, as in a plane wave propagating along the z axis, then:

$A(r')={\frac {-\partial }{\partial z'}}\int _{z'}^{\infty }dSA\left(\mathbf {0} ,t-{\frac {S}{c}}\right)=A\left(\mathbf {\mathbf {0} } ,t'-{\frac {z'}{c}}\right)$

This gives us uniform translation of waves at velocity c. More generally:

$A(r')={\frac {-1}{2\pi }}\int _{z=0}d^{2}r{\frac {\partial }{\partial z'}}\left({\frac {A\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)}{|\mathbf {r} -\mathbf {r} '|}}\right)$

$={\frac {-1}{2\pi }}\int _{z=0}d^{2}r\left({\frac {A\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)}{|\mathbf {r} -\mathbf {r} '|^{3}}}(-z')+{\frac {{\dot {A}}\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)}{|\mathbf {r} -\mathbf {r} '|c}}{\frac {-z'}{|\mathbf {r} -\mathbf {r} '|}}\right)$

$A(r')={\frac {-1}{2\pi }}\int _{z=0}d^{2}r\left({\frac {A\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)}{|\mathbf {r} -\mathbf {r} '|^{3}}}(-z')+{\frac {1}{c}}{\frac {{\dot {A}}\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)}{|\mathbf {r} -\mathbf {r} '|^{2}}}(-z')\right)$

In our case, we consider only those waves which drop off as ${\frac {1}{r'}}\quad$, so

$A(r')={\frac {z'}{2\pi c}}\int _{z=0}d^{2}r\left({\frac {{\dot {A}}\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)}{|\mathbf {r} -\mathbf {r} '|^{2}}}\right)$

In cylindrical coordinates, $d^{2}r=rdrd\phi \quad$. Without loss of generality, we consider a harmonic solution with a particular frequency ω = kc.

${\dot {A}}\left(\mathbf {r} ,t'-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}\right)={\dot {A}}(\mathbf {r} ,0)e^{-ik(t'c-|\mathbf {r} -\mathbf {r} '|)}$

$A(r')={\frac {ikz'}{2\pi }}\,e^{-i\omega t'}\int _{z=0}rdrd\phi \,{\frac {e^{ik|\mathbf {r} -\mathbf {r} '|)}}{|\mathbf {r} -\mathbf {r} '|^{2}}}A_{0}(\mathbf {r} ,0)$

Special Case

Picture an opaque screen with a circular aperture of radius a.

Let${\mathcal {J}}(r')=\int _{0}^{a}rdr\int _{0}^{2\pi }d\phi \,{\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{|\mathbf {r} -\mathbf {r} '|^{2}}}$

Then $A(r')={\frac {z'{\dot {A_{0}}}}{2\pi c}}e^{-ikct'}{\mathcal {J}}(r')$

But $|\mathbf {r} -\mathbf {r} '|={\sqrt {(x-x')^{2}+(y-y')^{2}+z'^{2}}}$

$={\sqrt {r^{2}+r'^{2}+2r\rho ^{2}\cos \phi }}$

$=r'-{\frac {2r\rho '\cos \phi }{2r'}},{\frac {\rho '}{r'}}=\sin {\theta }'$

so that $|\mathbf {r} -\mathbf {r} '|=r'-r\cos {\phi }\sin {\theta }'$ and ${\frac {1}{|\mathbf {r} -\mathbf {r} '|^{2}}}\approx {\frac {1}{r'^{2}}}\left(1+{\frac {2r\sin \theta '\cos \phi }{r'}}\right)$

In this particular case, we are dealing with far-field effects only, so ${\frac {2r\sin \theta '\cos \phi }{r'}}\rightarrow 0$ and ${\frac {1}{|\mathbf {r} -\mathbf {r} '|^{2}}}\approx {\frac {1}{r'^{2}}}$

So, ${\mathcal {J}}(r')=\int _{0}^{a}rdr\int _{0}^{2\pi }d\phi \,{\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{|\mathbf {r} -\mathbf {r} '|}}={\frac {e^{ikr'}}{r'^{2}}}\int _{0}^{a}rdr\int _{0}^{2\pi }d\phi \,e^{-ikr\sin {\theta }'\cos {\phi }}$

The integral $\int _{0}^{2\pi }d\phi \,e^{-ikr\sin {\theta }'\cos {\phi }}$ is the integral representation of the zero order Bessel function of the first kind with $kr\sin {\theta }'\quad$ as the argument. This gives us the equation:

${\mathcal {J}}(r')={\frac {e^{ikr'}}{r'^{2}}}\int _{0}^{a}rdr2\pi J_{0}(kr\sin {\theta }')$

To simplify the math, we make use of the fact that we can represent this Bessel functions as the derivative of a Bessel function of a different order. In general, the formula to compute this derivative is

$z^{v-k}J_{v-k}(z)=\left({\frac {1}{z}}{\frac {\partial }{\partial z}}\right)^{k}z^{v}J_{v}(z)$

In this case, we take $v=k=1\quad$ and $z=kr\sin {\theta }'\quad$. So

$J_{0}(kr\sin {\theta }')=\left({\frac {1}{kr\sin {\theta }'}}{\frac {\partial }{\partial (kr\sin {\theta }')}}\right)(kr\sin {\theta }')J_{1}(kr\sin {\theta }')$

This gives us the equation

${\mathcal {J}}(r')=2\pi {\frac {e^{ikr'}}{r'^{2}}}\int _{0}^{a}rdr\left({\frac {1}{kr\sin {\theta }'}}{\frac {\partial }{\partial (kr\sin {\theta }')}}\right)(kr\sin {\theta }')J_{1}(kr\sin {\theta }')$

Let $x=kr\sin {\theta '}\quad$ so that

${\mathcal {J}}(r')=2\pi {\frac {e^{ikr'}}{k^{2}\sin ^{2}{\theta }'r'^{2}}}\int _{0}^{ka\sin {\theta '}}dx{\frac {d}{dx}}xJ_{1}(x)$

${\mathcal {J}}(r')=2\pi {\frac {e^{ikr'}}{k\sin {\theta }'r'^{2}}}\left[aJ_{1}(ka\sin {\theta }')-0J_{1}(0k\sin {\theta }')\right]=2\pi {\frac {e^{ikr'}}{k\sin {\theta }'r'^{2}}}aJ_{1}(ka\sin {\theta }')$

and $A(r')={\frac {z'{\dot {A_{0}}}}{2\pi c}}e^{-i\omega t'}2\pi {\frac {e^{ikr'}}{k\sin {\theta }'r'^{2}}}aJ_{1}(ka\sin {\theta }')={\frac {z'{\dot {A_{0}}}a}{c}}{\frac {e^{ikr'-i\omega t'}}{k\sin {\theta }'r'^{2}}}J_{1}(ka\sin {\theta }')$

To find the angle to the diffraction minimum, we must find the zeroes of this amplitude function. This will occur when $J_{1}(ka\sin {\theta }')=0\quad$

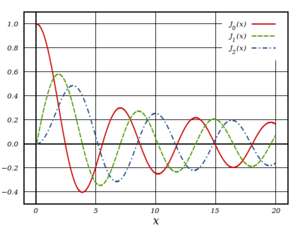
Plot of Bessel function of the first kind, J_α(x), for integer orders α=0,1,2.

To the right is a graph of three Bessel functions of the first order, specifically $J_{0}(x),J_{1}(x),andJ_{2}(x)\quad$. As it is shown, the first zero of $J_{1}(x)\quad$ will
occur at $x=0\quad$. This will correspond to the center of the pattern, at $\theta =0\quad$. Here, we would expect a bright spot, so $A(r')\quad$ should be positive and finite. At $\theta =0\quad$ the term ${\frac {J_{1}(ka\sin {\theta }')}{\sin {\theta }'}}$ is positive and finite, so this expression gives the correct amplitude at $\theta =0\quad$. The next zero of $J_{1}(x)\quad$ corresponds to the first minumum of the diffraction pattern. In this case, this zero occurs at x=3.832. So, $ka\sin {\theta }'=3.832\quad$ . Since$k={\frac {2\pi }{\lambda }}\quad$ and $a={\frac {D}{2}}\quad$

${\frac {2\pi D\sin {\theta }'}{2\lambda }}=3.832\rightarrow \sin {\theta }'={\frac {1.22\lambda }{D}}$