From the 3![]() data sample,
data sample, ![]() events are selected by requiring
that there is no
events are selected by requiring
that there is no ![]() in the event and that
in the event and that
![]() candidates from 2
candidates from 2![]() pairs are constrained to
pairs are constrained to ![]() of the
of the ![]() mass (0.5
mass (0.5
![]() 0.6
0.6 ![]() ).
We do not require just the presence of the
).
We do not require just the presence of the ![]() because
because ![]() production
is 50 times larger than
production
is 50 times larger than ![]() . Without cutting on the
. Without cutting on the ![]() ,
the
,
the ![]() signal competes with the
signal competes with the ![]() combinatoric background.
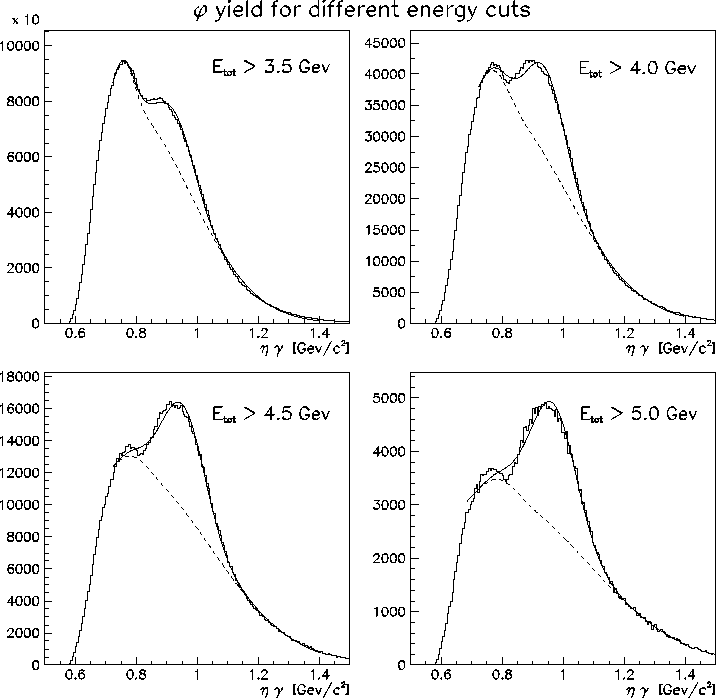
The invariant mass distribution of 3
combinatoric background.
The invariant mass distribution of 3![]() is then formed for different
minimum total energy in the LGD. These distributions
for 4 different energy thresholds are shown in Fig. 1,
where one can see how the
is then formed for different
minimum total energy in the LGD. These distributions
for 4 different energy thresholds are shown in Fig. 1,
where one can see how the ![]() peak becomes more prominent when
the total energy threshold is increased.
peak becomes more prominent when
the total energy threshold is increased.
The number of ![]() is found from the fit of these distributions to
3 Gaussians: one corresponding to the residual
is found from the fit of these distributions to
3 Gaussians: one corresponding to the residual ![]() peak,
one broad corresponding to the background (BG)
and the third one for the
peak,
one broad corresponding to the background (BG)
and the third one for the ![]() . To keep the number of parameters small,
the position of the background Gaussian is set to be equal to the position of
the
. To keep the number of parameters small,
the position of the background Gaussian is set to be equal to the position of
the ![]() peak, while the width of the BG is fixed to the
peak, while the width of the BG is fixed to the ![]() width by
width by
![]() . In addition,
the width of
. In addition,
the width of ![]() is kept constant during fitting,
is kept constant during fitting,
![]() .
Constants a and b are adjusted until good fits with reasonable
looking background is found. Obtained
.
Constants a and b are adjusted until good fits with reasonable
looking background is found. Obtained ![]() mass, width and yield for
different energy cuts are given in the Table 1.
mass, width and yield for
different energy cuts are given in the Table 1.
|
|
|
|
|||||
| 3.5 | 0.931 | 0.065 | 555513.0 | ||||
| 4.0 | 0.943 | 0.065 | 460076.0 | ||||
| 4.5 | 0.954 | 0.070 | 228128.0 | ||||
| 5.0 | 0.967 | 0.075 | 87140.4 |
 |