Difference between revisions of "Target Diamond Structural Analysis"
(Fixing various minor problems) |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
__TOC__ | __TOC__ | ||
| − | + | == Probing the Target Diamond's Structure == | |
| − | |||
| − | |||
| − | |||
| − | == Probing the Diamond's Structure == | ||
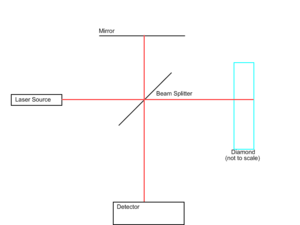
[[Image:01 Apparatus with Red Laser.png|thumb|The Michelson interferometer to be used. The diamond is not to scale.]] | [[Image:01 Apparatus with Red Laser.png|thumb|The Michelson interferometer to be used. The diamond is not to scale.]] | ||
| − | We must be able to determine the precise thickness and shape of the diamond chip. Because it is tiny (on the order of 50 microns thick), conventional measurements are impossible. Instead, we will use a modified [http://en.wikipedia.org/wiki/Michelson_interferometer Michelson interferometer]. In our design, we will replace one of the mirrors with the target diamond chip. In this modified design, the plane wave returned to the detector will be a combination of three waves (neglecting internal reflection): one reflected off the front of the diamond, one reflected off the back of the diamond, and one reflected off the remaining mirror. However, all that the detector can record is the wave's | + | We must be able to determine the precise thickness and shape of the diamond chip. Because it is tiny (on the order of 50 microns thick), conventional measurements are impossible. Instead, we will use a modified [http://en.wikipedia.org/wiki/Michelson_interferometer Michelson interferometer]. In our design, we will replace one of the mirrors with the target diamond chip. In this modified design, the plane wave returned to the detector will be a combination of three waves (neglecting internal reflection): one reflected off the front of the diamond, one reflected off the back of the diamond, and one reflected off the remaining mirror. However, all that the detector can record is the wave's intensity. From this, we need to extract thickness and shape. |
== The Diamond and Light Waves == | == The Diamond and Light Waves == | ||
| − | Both the front and back planes of the diamond are two-dimensional surfaces in three-dimensional space. The recorded | + | Both the front and back planes of the diamond are two-dimensional surfaces in three-dimensional space. The recorded intensities will form a two-dimensional graph and record intensity at points across the diamond's surface. Basically, the light wave can be treated as a massive grid of one-dimensional waves normal to the diamond. All of the following calculations are applied to the recorded intensity of one of these waves, which is the intensity at one specific point on the diamond. |
We will be neglecting all sources of error during these calculations. They will be reintroduced after we have obtained our basic calculations. | We will be neglecting all sources of error during these calculations. They will be reintroduced after we have obtained our basic calculations. | ||
| Line 23: | Line 17: | ||
<math>\Psi = A _{laser} \sin ( \omega t + d ) \,</math> | <math>\Psi = A _{laser} \sin ( \omega t + d ) \,</math> | ||
| − | where <math> A _{laser} </math> is the | + | where <math> A _{laser} </math> is the intensity of the initial laser beam, <math>\omega</math> is the frequency, t is time, d is the phase-shift, and C is a constant dependent on the reflectivity of all surfaces the laser intercepts. |
We have a sum of three waves, which can be expressed as | We have a sum of three waves, which can be expressed as | ||
| Line 35: | Line 29: | ||
(For simplicity, we will say that the wave leaving the mirror has not been phase-shifted, as above.) | (For simplicity, we will say that the wave leaving the mirror has not been phase-shifted, as above.) | ||
| − | == Ideal | + | == Ideal Intensity Calculation == |
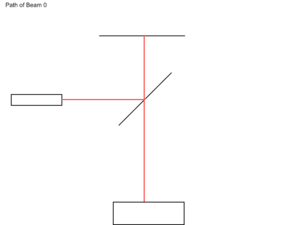
| − | + | [[Image:03 Apparatus for Beam 00.png|thumb|The zeroth wave path. Although some light passes through the splitter, it is lost, cannot affect the experiment, and therefore is not illustrated.]] | |
| − | The mirror has a coefficient of reflection r = 1 (it reflects all the light and does not transmit any), so we are only concerned with the half-silvered mirror. The recorded | + | Because all three waves are reflections of the same original wave, they all have the same wavelength. However, the processes of reflection and transmission will modify the ''intensity'' of each wave. By removing the diamond and reflecting the laser solely off of the mirror, we will be able to calculate the intensity of the initial light after it has reflected off the mirror and beam splitter once and been transmitted through the splitter once. |
| + | |||
| + | The mirror has a coefficient of reflection r = 1 (it reflects all the light and does not transmit any), so we are only concerned with the half-silvered mirror. The recorded intensity will be equal to <math> C _0 A _{laser} </math>. Because all beams that the detector will recieve will reflect off of and pass through the splitter once, we can create a new intensity variable A such that | ||
<math> A = A _{laser} C _0 \,</math> | <math> A = A _{laser} C _0 \,</math> | ||
| − | Because of this, we will never be dealing with the | + | Because of this, we will never be dealing with the intensity of the original laser. This will have no effect on the calculations, but it is important to remember that our value <math> A </math> is ''not'' the same as <math> A _{laser} </math>. |
== Ideal Thickness Calculation == | == Ideal Thickness Calculation == | ||
| − | [[Image:04 Appa for Beam 01.png|thumb|The first wave | + | [[Image:04 Appa for Beam 01.png|thumb|The first wave path. Although some light reflects off the splitter, it is lost, cannot affect the experiment, and therefore is not illustrated.]] |
To find the thickness of the diamond, we ideally only need the first two waves. To remove the third wave, which reflects from the mirror, we can simply remove the mirror. | To find the thickness of the diamond, we ideally only need the first two waves. To remove the third wave, which reflects from the mirror, we can simply remove the mirror. | ||
| − | The combined wave equation is unimportant, since we only record its | + | The combined wave equation is unimportant, since we only record its intensity, which is |
| − | <math>A^2 _{12} = C _1 A^2 + C _2 A^2 + 2 C _1 C _2 A^2 \cos ( d _2 - d _1 ) </math> | + | <math>A^2 _{12} = C _1 ^2 A^2 + C _2 ^2 A^2 + 2 C _1 C _2 A^2 \cos ( d _2 - d _1 ) </math> |
| − | <math>A^2 _{12} / A^2 = C _1 + C _2 + 2 C _1 C _2 \cos ( d _2 - d _1 ) </math> | + | <math>A^2 _{12} / A^2 = C _1 ^2 + C _2 ^2 + 2 C _1 C _2 \cos ( d _2 - d _1 ) </math> |
Because the wave reflecting off the back of the diamond travels through the diamond twice, the term <math> d _2 - d _1 </math> is twice the thickness of the diamond, in radians. Because this measurement is in unhelpful units, we can multiply it by the wavelength <math> \lambda </math> and divide by <math> 2 \pi </math> for the thickness <math> \tau </math> in meters. | Because the wave reflecting off the back of the diamond travels through the diamond twice, the term <math> d _2 - d _1 </math> is twice the thickness of the diamond, in radians. Because this measurement is in unhelpful units, we can multiply it by the wavelength <math> \lambda </math> and divide by <math> 2 \pi </math> for the thickness <math> \tau </math> in meters. | ||
| Line 63: | Line 59: | ||
Therefore, we can rewrite the earlier equation in terms of <math> \tau </math>: | Therefore, we can rewrite the earlier equation in terms of <math> \tau </math>: | ||
| − | <math>A^2 _{12} / A^2 = C _1 + C _2 + 2 C _1 C _2 \cos ( \frac{4 \pi \tau}{\lambda} ) </math> | + | <math>A^2 _{12} / A^2 = C _1 ^2 + C _2 ^2 + 2 C _1 C _2 \cos ( \frac{4 \pi \tau}{\lambda} ) </math> |
== Ideal Shape Calculation == | == Ideal Shape Calculation == | ||
| − | Of course, thickness is not the only thing we need. After calculating <math> \tau </math> and uncovering the mirror, we will also detect the third laser reflection. We can calculate that the | + | Of course, thickness is not the only thing we need. After calculating <math> \tau </math> and uncovering the mirror, we will also detect the third laser reflection. We can calculate that the intensity of this new combined wave will be |
<math>A^2 _{012} = C^2 _0 A^2 + C^2 _1 A^2 + C^2 _2 A^2 + 2 C _1 C _2 A^2 \cos ( d _2 - d _1 ) + 2 C _0 C _1 A^2 \cos ( - d _1 ) + 2 C _0 C _2 A^2 \cos ( - d _2 ) </math> | <math>A^2 _{012} = C^2 _0 A^2 + C^2 _1 A^2 + C^2 _2 A^2 + 2 C _1 C _2 A^2 \cos ( d _2 - d _1 ) + 2 C _0 C _1 A^2 \cos ( - d _1 ) + 2 C _0 C _2 A^2 \cos ( - d _2 ) </math> | ||
| + | |||
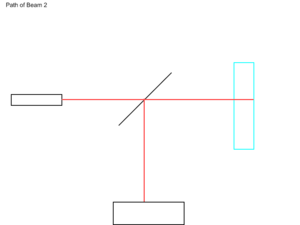
| + | [[Image:04 Appa for Beam 02.png|thumb|The second wave path. Note that the wave reflects off the back plane of the diamond instead of the front.]] | ||
Although this equation looks very complicated, we know that | Although this equation looks very complicated, we know that | ||
| Line 99: | Line 97: | ||
== Compensating for Internal Reflection == | == Compensating for Internal Reflection == | ||
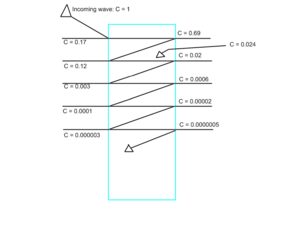
| − | [[Image:02 Internal Reflection with Labels.png|thumb|Internal reflection, where C is a coefficient to be multiplied by the | + | [[Image:02 Internal Reflection with Labels.png|thumb|Internal reflection of the diamond, where C is a coefficient to be multiplied by the incoming intensity. The angles have been exaggerated from zero degrees. The diagram also shows that all error comes from about two percent of the intensity.]] |
Realistically, the laser will not miraculously split in two upon reaching the diamond, creating one wave that reflects back and a second that reflects off of the back of the diamond and then passes perfectly through the front. Internal reflection will occur; we must calculate how much there will be and whether or not we must compensate for it. | Realistically, the laser will not miraculously split in two upon reaching the diamond, creating one wave that reflects back and a second that reflects off of the back of the diamond and then passes perfectly through the front. Internal reflection will occur; we must calculate how much there will be and whether or not we must compensate for it. | ||
| Line 174: | Line 172: | ||
Once again, the terms become very small very quickly. Because even the largest internal-reflection induced term (<math> 2 C _2 C _3 </math>) is more than an order of magnitude smaller than the needed terms, we can treat all internal reflection as error and ignore it. | Once again, the terms become very small very quickly. Because even the largest internal-reflection induced term (<math> 2 C _2 C _3 </math>) is more than an order of magnitude smaller than the needed terms, we can treat all internal reflection as error and ignore it. | ||
| − | This rapid decrease in | + | This rapid decrease in intensity is primarily because much of the initial intensity is completely lost during the reflection process, since 83% of any remaining intensity is lost each time the wave reflects off of the back of the diamond. This decrease is ''very'' significant. For example, when the wave <math> \Psi _2 </math> exits the diamond, the light reflected back into the diamond has an intensity less than three percent of the original wave, and 83% of ''this'' is lost when the wave reflects off of the back of the diamond, leaving less than half a percent of the initial intensity to make up all errors. |
== Interference == | == Interference == | ||
| Line 180: | Line 178: | ||
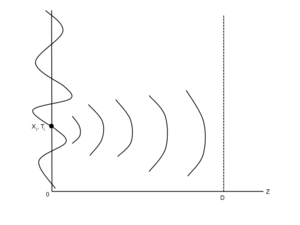
[[Image:06 Spherical Propogation.png|thumb|Each point on the wavefront generates spherical wavelets. Note that the waveform is not uniform.]] | [[Image:06 Spherical Propogation.png|thumb|Each point on the wavefront generates spherical wavelets. Note that the waveform is not uniform.]] | ||
| − | The | + | The propagating wavefront generates spherical wavelets as it propogates. What we want to know is what the wave at the initial point <math> f(x,y,0,t) </math> will look like at <math>f(x,y,D,t)</math>. To do this, we can integrate over the product of this equation times a propagator g. |
<math> g( x_i, t_i, x_f, t_f)\,</math> | <math> g( x_i, t_i, x_f, t_f)\,</math> | ||
| − | Because the | + | Because the propagator is actually in terms of the <i>differences</i> between the x and t values, we will write the difference between the x-vectors as '''Δx''' and the difference between the times as <math>\Delta t</math>. |
The integral is therefore | The integral is therefore | ||
| − | <math>\int{dt_i} \int{f(x_i,t_i)g(\Delta \mathbf{x}, \Delta t) dx_i dy_i}</math> | + | <math>f (x_f,t_f) = \int{dt_i} \int{f(x_i,t_i)g(\Delta \mathbf{x}, \Delta t) dx_i dy_i}</math> |
| − | + | where <math>f(x_i,t_i)\,</math> is nothing more than the product of the phases of the incoming and outgoing waves and the intensity function. Because this equation only takes into account one incoming and one outgoing wave, we will need to recalculate the later equations using different f-functions for all outgoing waves and sum these results. Fortunately, as we discovered above, only the first and second outgoing waves are relevant. | |
| − | |||
| − | <math>f(x_i,t_i)\,</math> | ||
| − | |||
| − | is nothing more than the product of the phases of the incoming and outgoing waves and the | ||
Calculation of g proves more challenging. We know the wave equation | Calculation of g proves more challenging. We know the wave equation | ||
| − | <math>\frac{d^2y}{dt^2} - c^2\ | + | <math>\frac{d^2y}{dt^2} - c^2\nabla^2 = 0</math> |
However, this is for a uniform, sourceless wave. Like most generalizations, this is an unrealistic situation in the real world. What we need is a function that can generate a brief pulse. This sounds like a delta function. | However, this is for a uniform, sourceless wave. Like most generalizations, this is an unrealistic situation in the real world. What we need is a function that can generate a brief pulse. This sounds like a delta function. | ||
| − | <math>\frac{d^2g}{dt^2} - c^ | + | <math>\frac{d^2g}{dt^2} - c^2nabla^2 = \delta^3(\Delta \mathbf{x})\delta(\Delta t)</math> |
This is not an easy equation to solve without using a Fourier transform. Therefore, we'll do just that, with G as the transformed function. | This is not an easy equation to solve without using a Fourier transform. Therefore, we'll do just that, with G as the transformed function. | ||
| Line 210: | Line 204: | ||
Therefore, | Therefore, | ||
| − | <math>g(\Delta \mathbf{x},\Delta t) = \frac{1}{4\pi^2} \int{G(\mathbf{k},\omega)e^{ | + | <math>g(\Delta \mathbf{x},\Delta t) = \frac{1}{4\pi^2} \int{G(\mathbf{k},\omega)e^{i\mathbf{k}\cdot\Delta x}e^{-i\omega \Delta t}d^3k d\omega}</math> |
We will then need to plug this function into the earlier equation. To make this easier, we know that the four-dimensional delta function on the right-hand side can be simplified. | We will then need to plug this function into the earlier equation. To make this easier, we know that the four-dimensional delta function on the right-hand side can be simplified. | ||
| Line 218: | Line 212: | ||
Now, we have an equation with integrals on both sides. Since both of these integrals have the same limits and integrands, they must be integrals of equal functions. We can simply drop the integrals. | Now, we have an equation with integrals on both sides. Since both of these integrals have the same limits and integrands, they must be integrals of equal functions. We can simply drop the integrals. | ||
| − | <math> \frac{d^2}{dt^2} \left(\frac{1}{4\pi^2} G(\mathbf{k},\omega)e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}\right)-c^ | + | <math> \frac{d^2}{dt^2} \left(\frac{1}{4\pi^2} G(\mathbf{k},\omega)e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}\right)-c^2nabla^2\left(\frac{1}{4\pi^2} G(\mathbf{k},\omega)e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}\right) = \frac{1}{16\pi^4} e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}</math> |
| + | |||
| + | This is a complicated equation, but it can be solved for G. | ||
| + | |||
| + | <math>G(\mathbf{k},\omega) = \frac{-1}{4\pi^2}\left(\frac{1}{c^2k^2-\omega^2}\right)</math> | ||
| − | + | Once G is calculated, we can apply an inverse Fourier transform and find g; we can then plug this into | |
<math>\int{dt_i} \int{f(x_i,t_i)g(\Delta x, \Delta t) dx_i dy_i}</math> | <math>\int{dt_i} \int{f(x_i,t_i)g(\Delta x, \Delta t) dx_i dy_i}</math> | ||
| Line 228: | Line 226: | ||
== Color of the Laser == | == Color of the Laser == | ||
| − | The laser used must have a wavelength | + | The laser used must have a wavelength less than the maximum expected defect of the diamond. Because any defects will be extremely small (on the order of one micron thick), we need light with a wavelength of around 500 nm. We could use either a green or red laser. Once expected error is calculated, we will be able to calculate expected error from the less accurate red light, and determine whether or not it would be usable. |
== Future Updates == | == Future Updates == | ||
Latest revision as of 21:12, 14 May 2009
Probing the Target Diamond's Structure
We must be able to determine the precise thickness and shape of the diamond chip. Because it is tiny (on the order of 50 microns thick), conventional measurements are impossible. Instead, we will use a modified Michelson interferometer. In our design, we will replace one of the mirrors with the target diamond chip. In this modified design, the plane wave returned to the detector will be a combination of three waves (neglecting internal reflection): one reflected off the front of the diamond, one reflected off the back of the diamond, and one reflected off the remaining mirror. However, all that the detector can record is the wave's intensity. From this, we need to extract thickness and shape.
The Diamond and Light Waves
Both the front and back planes of the diamond are two-dimensional surfaces in three-dimensional space. The recorded intensities will form a two-dimensional graph and record intensity at points across the diamond's surface. Basically, the light wave can be treated as a massive grid of one-dimensional waves normal to the diamond. All of the following calculations are applied to the recorded intensity of one of these waves, which is the intensity at one specific point on the diamond.
We will be neglecting all sources of error during these calculations. They will be reintroduced after we have obtained our basic calculations.
Light is a wave, and can be expressed as
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi = A _{laser} \sin ( \omega t + d ) \,}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A _{laser} } is the intensity of the initial laser beam, is the frequency, t is time, d is the phase-shift, and C is a constant dependent on the reflectivity of all surfaces the laser intercepts.
We have a sum of three waves, which can be expressed as
(For simplicity, we will say that the wave leaving the mirror has not been phase-shifted, as above.)
Ideal Intensity Calculation
Because all three waves are reflections of the same original wave, they all have the same wavelength. However, the processes of reflection and transmission will modify the intensity of each wave. By removing the diamond and reflecting the laser solely off of the mirror, we will be able to calculate the intensity of the initial light after it has reflected off the mirror and beam splitter once and been transmitted through the splitter once.
The mirror has a coefficient of reflection r = 1 (it reflects all the light and does not transmit any), so we are only concerned with the half-silvered mirror. The recorded intensity will be equal to . Because all beams that the detector will recieve will reflect off of and pass through the splitter once, we can create a new intensity variable A such that
Because of this, we will never be dealing with the intensity of the original laser. This will have no effect on the calculations, but it is important to remember that our value is not the same as .
Ideal Thickness Calculation
To find the thickness of the diamond, we ideally only need the first two waves. To remove the third wave, which reflects from the mirror, we can simply remove the mirror.
The combined wave equation is unimportant, since we only record its intensity, which is
Because the wave reflecting off the back of the diamond travels through the diamond twice, the term is twice the thickness of the diamond, in radians. Because this measurement is in unhelpful units, we can multiply it by the wavelength and divide by for the thickness in meters.
Therefore, we can rewrite the earlier equation in terms of :
Ideal Shape Calculation
Of course, thickness is not the only thing we need. After calculating and uncovering the mirror, we will also detect the third laser reflection. We can calculate that the intensity of this new combined wave will be
Although this equation looks very complicated, we know that
so
To further simplify, we need a "shape term". This term will represent the difference in the distance traveled by waves 0 and 1. If the phase-shift between 0 and 1 is constant, the diamond is flat; otherwise, it is deformed by some distance expressed by s.
We can rewrite this in terms of :
Simplifying our initial equation, we find that
Because the cosine is an even function, we can slightly simplify this further.
This equation, athough complicated, is completely solvable, as the only unknown is the s-term.
Compensating for Internal Reflection
Realistically, the laser will not miraculously split in two upon reaching the diamond, creating one wave that reflects back and a second that reflects off of the back of the diamond and then passes perfectly through the front. Internal reflection will occur; we must calculate how much there will be and whether or not we must compensate for it.
The coefficient of reflectivity R can be calculated from
where is the index of refraction for air and is the index of refraction for diamond. We can look these up and calculate R:
We also need the coefficient of transmission T. However, because , calculation is easy.
This tells us that about 83% of the laser will be transmitted through the diamond at each reflection. This tells us :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _1 = R = 0.17189 \,}
For Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _2 } , we must take into account two transmissions and one reflection. The calculation is easy:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _2 = R T^2 = 0.117876 \,}
We can continue and calculate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _3} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _4} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _5} .
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _3 = R^3 T^2 = 0.003483 \,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _4 = R^5 T^2 = 0.000103 \,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _5 = R^7 T^2 = 0.000003 \,}
Generally, for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _n } where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n > 2 } :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _n = T^2 R^{2(n-1)-1} \,}
Using just the five waves Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _1 } to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C _5 } to begin with, we can recalculate our shape term.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A^2 _{12345}}{A ^2} = C^2 _1 + C^2 _2 + C^2 _3 + C^2 _4 + C^2 _5 + 2 C _1 C _2 \cos ( d _2 - d _1 ) }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle + 2 C _1 C _3 \cos ( d _3 - d _1 ) + 2 C _1 C _4 \cos ( d _4 - d _1 ) + 2 C _1 C _5 \cos ( d _5 - d _1 ) \,}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle + 2 C _2 C _3 \cos ( d _3 - d _2 ) + 2 C _2 C _4 \cos ( d _4 - d _2 ) + 2 C _2 C _5 \cos ( d _5 - d _2 ) \,}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle + 2 C _3 C _4 \cos ( d _4 - d _3 ) + 2 C _3 C _5 \cos ( d _5 - d _3 )+ 2 C _4 C _5 \cos ( d _5 - d _4 ) \,}
This is an unnerving equation. However, we only have eleven C-terms that need to be calculated. We can begin with the sum of C-terms and compare it to the idealized version.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^2 _1 + C^2 _2 + C^2 _3 + C^2 _4 + C^2 _5 = 0.043453\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^2 _1 + C^2 _2 = 0.043441\,}
Because the difference between these terms is three orders of magnitude less than the measurement, we can count it as error and do not need to compensate for it.
Next, we need to calculate all of the inner products.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _1 C _2 = 0.0405\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _1 C _3 = 0.0012\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _1 C _4 = 0.0000\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _1 C _5 = 0.0000\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _2 C _3 = 0.0008\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _2 C _4 = 0.0000\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _2 C _5 = 0.0000\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _3 C _4 = 0.0000\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _3 C _5 = 0.0000\,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _4 C _5 = 0.0000\,}
Once again, the terms become very small very quickly. Because even the largest internal-reflection induced term (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 C _2 C _3 } ) is more than an order of magnitude smaller than the needed terms, we can treat all internal reflection as error and ignore it.
This rapid decrease in intensity is primarily because much of the initial intensity is completely lost during the reflection process, since 83% of any remaining intensity is lost each time the wave reflects off of the back of the diamond. This decrease is very significant. For example, when the wave Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi _2 } exits the diamond, the light reflected back into the diamond has an intensity less than three percent of the original wave, and 83% of this is lost when the wave reflects off of the back of the diamond, leaving less than half a percent of the initial intensity to make up all errors.
Interference
The propagating wavefront generates spherical wavelets as it propogates. What we want to know is what the wave at the initial point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,y,0,t) } will look like at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,y,D,t)} . To do this, we can integrate over the product of this equation times a propagator g.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g( x_i, t_i, x_f, t_f)\,}
Because the propagator is actually in terms of the differences between the x and t values, we will write the difference between the x-vectors as Δx and the difference between the times as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} .
The integral is therefore
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f (x_f,t_f) = \int{dt_i} \int{f(x_i,t_i)g(\Delta \mathbf{x}, \Delta t) dx_i dy_i}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_i,t_i)\,} is nothing more than the product of the phases of the incoming and outgoing waves and the intensity function. Because this equation only takes into account one incoming and one outgoing wave, we will need to recalculate the later equations using different f-functions for all outgoing waves and sum these results. Fortunately, as we discovered above, only the first and second outgoing waves are relevant.
Calculation of g proves more challenging. We know the wave equation
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2y}{dt^2} - c^2\nabla^2 = 0}
However, this is for a uniform, sourceless wave. Like most generalizations, this is an unrealistic situation in the real world. What we need is a function that can generate a brief pulse. This sounds like a delta function.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2g}{dt^2} - c^2nabla^2 = \delta^3(\Delta \mathbf{x})\delta(\Delta t)}
This is not an easy equation to solve without using a Fourier transform. Therefore, we'll do just that, with G as the transformed function.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\mathbf{k},\omega) = \frac{1}{4\pi^2} \int{g(\Delta \mathbf{x},\Delta t)e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}d^3x dt}}
Therefore,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(\Delta \mathbf{x},\Delta t) = \frac{1}{4\pi^2} \int{G(\mathbf{k},\omega)e^{i\mathbf{k}\cdot\Delta x}e^{-i\omega \Delta t}d^3k d\omega}}
We will then need to plug this function into the earlier equation. To make this easier, we know that the four-dimensional delta function on the right-hand side can be simplified.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta^4(\Delta \mathbf{x},\Delta t) = \frac{1}{16\pi^4} \int{e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}d^3k d\omega}}
Now, we have an equation with integrals on both sides. Since both of these integrals have the same limits and integrands, they must be integrals of equal functions. We can simply drop the integrals.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2}{dt^2} \left(\frac{1}{4\pi^2} G(\mathbf{k},\omega)e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}\right)-c^2nabla^2\left(\frac{1}{4\pi^2} G(\mathbf{k},\omega)e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}\right) = \frac{1}{16\pi^4} e^{-i\mathbf{k}\cdot\Delta \mathbf{x}}e^{i\omega \Delta t}}
This is a complicated equation, but it can be solved for G.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\mathbf{k},\omega) = \frac{-1}{4\pi^2}\left(\frac{1}{c^2k^2-\omega^2}\right)}
Once G is calculated, we can apply an inverse Fourier transform and find g; we can then plug this into
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int{dt_i} \int{f(x_i,t_i)g(\Delta x, \Delta t) dx_i dy_i}}
and calculate the effects of the spherical wavelets.
Color of the Laser
The laser used must have a wavelength less than the maximum expected defect of the diamond. Because any defects will be extremely small (on the order of one micron thick), we need light with a wavelength of around 500 nm. We could use either a green or red laser. Once expected error is calculated, we will be able to calculate expected error from the less accurate red light, and determine whether or not it would be usable.
Future Updates
- Compensate for other sources of error
- Calculate expected error