Section IV.4: Beam Line and Tagger

The adjective `coherent' in coherent bremsstrahlung does not indicate that the photons in the beam are in a coherent state, as is light from a laser. Rather it refers to the coherent effect of multiple atoms in a crystal lattice in absorbing the recoil momentum from a high energy electron when it radiates a bremsstrahlung photon. In X-ray spectroscopy one encounters the same thing in the Mosbauer effect, except in that case the chief physical consequence is the disappearance of the recoil Doppler shift. Here the chief consequence is the enhancement of bremsstrahlung at those particular kinematics for which the recoil momentum matches one of the reciprocal lattice vectors of the crystal. Another useful way to view the process of coherent bremsstrahlung is as virtual Compton scattering. To the high energy electron, the atoms in the radiator appear as clouds of virtual photons. For a disoriented radiator material, the virtual photon spectrum is given simply by the atomic form factor, averaged over the different species in the material. If the radiator is a single crystal, however, the atomic form factor gets multiplied by the form factor of the crystal, which in the ideal case looks like a series of delta-functions located at the sites of the reciprocal lattice. In effect, the crystal provides a set of virtual laser beams, each one a standing wave tuned to a specific reciprocal lattice vector. In this view the process of hard bremsstrahlung is seen to be the same as Compton backscattering of laser light. For a more detailed discussion of the physics of coherent bremsstrahlung there are a number of good references [2-4].

The use of Compton backscattering of laser light as a photon source was earlier noted as ruled out by the limitation of high-power lasers and cavities to wavelengths above 100µm. The characteristic wavelength of the crystal photons is a few Angstroms, three orders of magnitude shorter. In this case, 180^o scattering would result in essentially 100% of the electron beam momentum being transfered to the photon in the lab frame. Unfortunately, however, the Compton cross section contains a factor of (q·p)¨² where q is the virtual photon momentum and p is that of the electron, which strongly favors incident photons with q nearly orthogonal to p. With reciprocal lattice vectors pointing in almost every direction, only those nearly perpendicular to the beam contribute appreciably to the scattering rate. This fact applies equally to ordinary bremsstrahlung; in fact, to a first approximation the bremsstrahlung spectrum from a single crystal is the same as from a disoriented radiator. The reason is that, if the sum over crystal momenta were replaced with a continuous integral, one would recover the ordinary bremsstrahlung result for isolated atoms. Beyond a few unit cells from the origin in reciprocal lattice space, the atomic form factor and kinematic factors become slowly varying on the scale of the lattice spacing, and the sum becomes indistinguishable from the integral. Besides that, the uncertainty principle requires that atoms localized at the sites in a crystal undergo fluctuations about their mean position. This has the effect of attenuating the discrete peaks in the crystal form factor at progressively higher-order crystal momenta, eventually washing them out and filling in the gaps between them, so that the sum deforms smoothly into the integral at high momentum transfer. Hence, the sum over crystal indices that yields the final photon spectrum can be separated into two parts: a discrete sum over a limited set of small crystal indices and an integral over the continuum of momentum transfer values beyond. The latter appears in the coherent bremsstrahlung beam as an ordinary 1/k bremsstrahlung spectrum, while the former appears as a set of peak structures superimposed upon it. The 1/k continuum, referred to as the incoherent component, is invariant as the crystal is rotated, whereas the coherent peaks change in position and intensity, depending on crystal orientation.

Fig. 2 Coherent bremsstrahlung spectrum, calculated for a diamond crystal radiator 20µm thick and a 100nA electron beam of 12GeV energy. Typical values were used for beam emittance and crystal mosaic spread.

A typical coherent bremsstrahlung spectrum is shown in Fig. 2. The distinction between incoherent and coherent components in the figure is artificial; it is there to show the part of the spectrum that shifts as the crystal is rotated. The vertical scale in the figure gives the photon rate for the given beam current and crystal thickness. Note that the intensity of the incoherent background is less than what would be obtained with an amorphous carbon radiator of the same thickness, because a part of the momentum transfer integral in the Bethe-Heitler formula has been moved into the discrete sum and contributes to the coherent part. The radiation length of diamond is actually an average over all orientations of the crystal. In the calculation for Fig. 2 the leading 400 lattice sites were included in the discrete part of the calculation, although it can be seen that only two or three of them contribute with sufficient intensity to be individually visible in the spectrum.

The presence of the large incoherent flux in Fig. 2 presents a significant handicap to a photoproduction experiment. Not only do the low energy photons produce background in the detector, but they diminish the polarization of the beam. The entire beam polarization appears in the coherent component; the underlying incoherent flux only serves to dilute the polarization. There is another difference between the two components that allows them to be separated to some extent. The kinematics of bremsstrahlung confines most of the intensity of the photon beam to forward angles within m/E radians of the incident electron direction. In the lab this is a small angle, but in the rest frame of the electron-photon system it subtends all angles in the forward hemisphere. A peak in the coherent component that corresponds to a single reciprocal lattice vector has two-body kinematics, so there is a well-defined relation between the emission angle and the energy of the emitted photon in the lab: emission at 0^o yields a maximum energy photon, with energy decreasing with increasing angle. This accounts for the shape of the coherent peaks in Fig. 2, with the sharp right-hand edge corresponding to 0^o emission and the tail to lower energies corresponding to scattering into higher angles.

The incoherent component, because it comes from a sum over momentum transfers at all angles, has essentially no correlation between photon energy and emission angle. This means that collimating away all photons beyond some angle _max < m/E uniformly attenuates the incoherent spectrum at all energies, whereas it preserves all of the coherent photons from the maximum energy for the given peak down to some cutoff. The kinematic relations for coherent bremsstrahlung are as follows,

	(1)
	(2)

Fig. 3 Coherent bremsstrahlung spectrum, calculated under the same conditions as in Fig. 2, after collimation. The upper curve is the uncollimated spectrum from Fig. 2. The middle curve corresponds to a 5mm diameter collimator placed 80m downstream of the radiator, or approximately 0.75 m/E in collimator half-angle. The lower curve corresponds to a 2mm collimator in the same position, approximately 0.30 m/E in half-angle.

The effects of collimation are demonstrated in the calculated spectra shown in Fig. 3. First, note that the collimation angles are very small, which requires a long flight path of order 100m in order that the collimator can be larger than the intrinsic beam spot size, otherwise the collimator is cutting in transverse coordinate instead of in angle. This distance is, in fact, a sensitive function of the electron beam emittance from the machine, and must be increased in inverse proportion to the beam emittance if the effectiveness of collimation is to be maintained. This issue, along with the associated demands placed on beam alignment and position stability, are taken up in more detail in the following section on the electron beam line.

Second, note that the cut imposed on the coherent peak by collimation does not produce a perfectly sharp edge as would be expected from two-body kinematics. This is because a collimator cuts on radius at some fixed position which translates into a cut on emission angle only in an approximate way, and is why the curves in Fig. 3 are labelled by their collimator size and distance individually rather than their ratio which is the approximate collimation angle. Multiple scattering by the electron in the radiator prior to emission and beam spot size and divergence are the major contributors to the error involved in interpreting a collimator as a cut in emission angle. All of these effects have been incorporated into the analytical calculation of the yields from a collimated coherent bremsstrahlung source that has been used in preparing this report. Crystal imperfections, which amount to an intrinsic spread in the direction of the incoming virtual photon, are also accounted for in the calculation.

Third, note that the relatively weak collimation at 5mm reduces the incoherent background without significantly affecting the coherent flux near the maximum, and thereby almost doubling the polarization of the beam at the peak relative to the uncollimated case. Further reducing the collimator diameter continues to narrow the peak and reduce the incoherent flux relative to the peak, albeit at some cost in peak intensity. In the case of the 2mm collimator, the peak polarization is essentially that of the coherent component alone. Although almost all of the photon beam energy is being absorbed at this point at the collimator, provided there is adequate shielding around the collimator the necessary flux in the collimated beam can be made up by increasing the electron beam current. The peak in Fig. 3 for a 2mm collimator contains 1M photons/s for an electron beam current of 100nA, which could be increased by a factor of up to 100 in the facility being planned for Hall D.

Fourth, note that the rate seen in the focal plane of the tagging spectrometer corresponds to the dotted curve in Fig. 3, regardless of the collimation. This means that collimating the bremsstrahlung beam increases the rate in the tagger focal plane relative to what is seen at the detector. For example, running with the 2mm collimator and 10 photons/s in the main coherent peak implies according to Fig. 3 a rate of 250MHz per GeV in the focal plane. Under these conditions, only a small part of the focal plane is in coincidence with the events of interest, which limits the rate of accidental tags to a reasonable level. For maximum flexibility, the full upper 25% of the tagging range must be designed to handle rates as high as this.

Fig. 4 Plane polarization of the coherent bremsstrahlung beam, calculated under the same conditions as in Fig. 3. The dashed lines indicate the trajectory of the peak polarization as the peak energy is swept across the focal plane by rotating the crystal.

The net polarization of the beam under different collimation conditions is shown in Fig. 4. The dashed curves show how the maximum polarization in the peak varies as the peak energy is changed by rotating the crystal. The polarization in all cases is zero at the endpoint. Without collimation it rises as (k-E), one power coming from the intensity of the coherent peak relative to the incoherent component going to zero linearly at the endpoint, and the other from the intrinsic polarization of the coherent photons also behaving like (k-E) near the endpoint. Collimation allows one to essentially isolate the coherent component, so that the polarization available to the experiment rises from zero at the endpoint in a linear fashion. The dashed curves in Fig. 4 demonstrate this point.

The ideal radiator would be a layered structure with a strong transverse fields that alternate between layers spaced about 50nm apart, thus simulating the standing wave in a cavity driven by a 15eV laser. While it is possible to construct ordered materials with unit cells as large as this, the self-shielding of atoms means that beyond the atomic length scale the residual fields are comparatively weak. Hence heterogeneous structures are not viable for use as a coherent radiator. Since the strong fields inside a solid are revealed at the atomic scale, the first requirement for a good radiator is that the unit cell be compact and closely packed. The best radiators are those with the smallest unit cells because these provide the best match between the atomic and the crystal form factors. This match is best for the light elements, and essentially prohibits the effectiveness of any materials heavier than carbon. An extensive survey of possible radiator materials is presented in Ref. [5]. In Table 1 is shown the figure of merit that those authors report for favored crystalline materials. The figure of merit is the product of the atomic times the crystal form factor evaluated at the leading peak, normalized to the value for diamond.

Table 1: Figure of merit of various materials that might be used as a coherent bremsstrahlung radiator. This table is reproduced from Table 2 in Ref. [5].

crystal	best reciprocal vector	P/Pdiamond
diamond	2,-2,0	1.00
beryllium	0,0,2	0.86
boron	2,0,8	0.38
silicon	2,-2,0	0.19
BeC	2,2,0	1.10

Table 1 shows that the list of viable materials for a crystal radiator is relatively short. Silicon would be an excellent choice from the point of view of price and fabrication, but unfortunately it is far inferior in terms of performance. Beryllium carbide is not a material that is familiar to the crystal growth industry, and nothing is known at present concerning its suitability for the growth of single crystals of large area. In general compound materials are more susceptible to radiation damage than are pure elements, which would argue in favour of diamond and beryllium metal. These two materials are comparable in terms of their performance. Most of the experience to date with coherent bremsstrahlung has been with diamond radiators. Extensive expertise for handling large diamond crystals exists within the gem industry. High quality monocrystals of 6mm x 6mm and as thin as 100µm were obtained at SLAC [1] by cleaving from a facet of a large gem. This was made possible by a contact that existed at the time with a friendly insider in the gem business. It is not clear at the present whether this success could be repeated in a cost effective way, and so it is important to consider beryllium as an alternative radiator material.

Beryllium metal is widely used in industry, being preferred for its high strength-to-weight ratio and robustness, in addition to its transparency to X-rays. Thin films of high-purity beryllium are routinely produced for vacuum window applications, which use some of the same vacuum deposition techniques that would be used for the growth of single crystals. As a radiator material, beryllium is distinguished as the metal with the highest Debye temperature, around 1400K. The Debye temperature measures the temperature at which the thermal motion of the atoms in the lattice reaches the level of the zero-point motion due to their confinement in the lattice, as dictated by the uncertainty principle. A high Debye temperature indicates a stiff crystal lattice, in which the atoms have little liberty to move and so have large momentum fluctuations, as dictated by the uncertainty principle.

A high Debye temperature is important for a bremsstrahlung radiator material for three reasons. First, the cross section for coherent bremsstrahlung from a discrete crystal momentum vector q contains a factor exp(-q / 4M_D) which reflects the fact that position fluctuations of atoms in the lattice diminish the coherent effect. This factor is near unity for the low-order crystal momenta provided that _D is sufficiently large. Second, the Debye temperature is, roughly speaking, a measure of the stability of the crystal structure and hence its readiness to form as a single crystal and to survive significant doses of radiation. Third, the radiator material will inevitably be heated by the beam, and will normally operate in vacuum well above the ambient temperature. A high Debye temperature means that there is a large range of temperatures over which the material may operate without degraded performance as a crystal radiator. The Debye temperature of diamond is about 2200K. Past experience has shown that diamond meets all of the requirements for a good crystal radiator. There is good reason to believe that beryllium would function almost as well at substantially less cost, but this remains to be proved.

Crystal thickness

The range of permissible thicknesses for a crystal radiator is bounded both from above and below. It is bounded from above by multiple scattering of the electron beam as it passes through the radiator, which causes the divergence of the incident beam to grow, thereby enlarging the photon beam spot on the collimator face and degrading the degree to which collimation discriminates against the incoherent component in favor of the coherent part. It is bounded from below by the fact that the crystal must be of some minimum thickness in order to achieve the full coherent gain. In the calculation of the coherent bremsstrahlung process one begins by assuming an infinite crystal, although practically it is presumed to mean only that the crystal is large compared to the some characteristic scale. It is important to identify what the characteristic scale is in this problem in order to know how thin one can make the crystal without hurting performance. In the analogous case of the Mosbauer effect, one can estimate the number of atoms participating in the collective absorption by looking at the emission time of the photon (lifetime of the radiating transition) and asking how many nuclei lie within the envelop of the photon wave packet. In the coherent bremsstrahlung process, the lifetime of the radiating system is given in the lab system by the uncertainty principle and by how far the electron energy deviates from its on-shell value between absorbing the virtual photon and emitting the real one. The latter quantity is almost exactly given by q_z, the virtual photon momentum component along the incident electron axis, which means that the electron travels a distance = c/q_z during the interaction. For a given coherent peak at normalized energy x in the photon spectrum, the coherence length is given by

(3)

in units of c. From this simple argument one sees that the coherent gain goes linearly to zero at the endpoint, a result that is borne out by the full QED calculation. One also sees that the lower limit on crystal thickness imposed by the coherence length depends upon both the electron beam energy and the photon energy. For a 12GeV beam energy and a 6GeV coherent photon the coherence length is 18nm, or about 50 unit cells for diamond. This shows that the coherence length does not impose a practical limit on how thin the radiator should be.

Fig. 5 Collimated coherent bremsstrahlung spectrum from a 1µA electron beam at 12GeV using diamond radiators of two different thicknesses. The calculation assumes a 2mm collimator located 80m from the radiator, and typical values for beam emittance and crystal quality.

The effects of multiple scattering are best presented by showing the calculated spectra for various radiator thicknesses. The diamond radiators used at SLAC were cleaved at approximately 100µm and then milled down to about 50µm using ion bombardment. In Fig. 5 is shown the photon spectrum for a 20µm and a 100µm radiator to demonstrate the effect. The 100µm spectrum is scaled down by a factor of 5 to facilitate the comparison. The calculation assumed a 2mm collimator located 80m downstream of the radiator. The loss in normalized intensity with the thicker radiator, as well as the broadening of the left edge of the peak, is due to the enlarging of the photon beam spot on the collimator face from multiple scattering of the electron beam in the crystal prior to radiation. A 100µm diamond crystal is roughly 10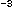 radiation lengths thick. It is reasonable to run with as thick a radiator as is permitted by multiple scattering considerations, in order to keep the beam current to a minimum and prolong as much as possible the lifetime of the crystal.

It has already been shown that in order to achieve appreciable coherent gain the crystal must be oriented so that the coherent peaks appear well below the end point. Eq. 2 then implies that the orientation must be such that the crystal momentum dotted with the beam momentum be of order m. Given a p of 12GeV and q of 10KeV, this requires that the two vectors must be within 100µr of perpendicular to each other and that, within a range of angles of that order, the coherent peak sweeps out nearly the full range in x from 0 to 1. Hence both the incident beam angle and the angle of the crystal radiator must be stable at the level of a few µr in order to have a stable photon beam for running. At least one of the two must be adjustable in steps that are small compared to 100µm in order to have the ability to position the coherent peak at the desired energy. These requirements are most simply achieved using a precision two-axis goniometer. Commercial devices of this type exist with step sizes as small as required for this application. With two-axis remote control the crystal can be reoriented in a matter of minutes to produce a coherent beam of any desired energy and in either vertical or horizontal plane polarization modes.

Thermal effects in the crystal mount and small variations in the beam tune from the accelerator make long term stability and reproducibility more difficult to achieve than adequate controls for the initial setup. For this reason it is important that there be sufficient diagnostics present to monitor the crystal orientation relative to the beam. This diagnostic is provided by the rates in the tagger focal plane counters. From Fig. 2 it is clear that the critical angle between the beam and the crystal, as well as the quality of the crystal, are accurately reflected in the position and sharpness of the coherent edge in the focal plane rate profile. Better than simply monitoring the critical angle, the tagger profile provides a direct look at the photon beam spectrum prior to collimation. This means that there is no need for an absolute alignment of the crystal and goniometer to this level of precision, because only relative accuracy is required. The second angle is non critical, typically of order a degree, and does not need to be monitored. If conditions require it, a feedback system could be put in place to correct for drifts seen in the tagger focal plane profile by periodically adjusting the goniometer setting within predefined limits. This would involve a slow control system, and does not need to be designed in advance.

Fig. 6 Coherent photon spectrum for three different values of the r.m.s. size of the virtual electron beam spot on the collimator. A 2mm diameter collimator 80m downstream of the radiator was used.

Fig. 6 shows how the collimated photon spectrum depends upon the r.m.s. size of the virtual electron beam spot on the collimator. When the spot size becomes comparable with the collimator aperture then the collimation is rendered ineffective, and the photon spectrum and polarization revert to their uncollimated values. The connection between focal spot size and beam emittance can be seen by noting that an upper bound is placed on the angular divergence of the beam at the radiator in order to maintain the same incidence angle with respect to the planes of the crystal for all electrons in the beam. Practically, the divergence does not broaden the coherent peak provided that it is kept below the mosaic spread of the crystal. A conservative value for the allowable angular divergence in the electron beam at the radiator would then be 20µm. Taken together with a 200µm r.m.s. spot size at the focus, this leads to an emittance of 50mm·µr at 12GeV. The 600µm spot size in Fig. 6 corresponds to an emittance of 150mm·µr and the 2mm spot to 0.5mm·mr.

Not only must the virtual electron spot be small enough to fit within the collimator aperture, but it must also be centered on the aperture and stable. In order to maintain a stable beam position on the collimator, the SLAC experiment [1] installed a segmented halo detector just upstream of the collimator and operated an active feedback loop to a vertical and horizontal pair of dipoles located just upstream of the radiator. From that distance a bend of only 10µr results in a shift of 1mm at the collimator position. Hence the beam alignment feedback system is effectively decoupled from the crystal orientation controls. Small deflections that are necessary to keep the beam centered on the collimator do not produce appreciable walk in the beam-crystal angle, and by using a goniometer to control the latter, the former can be operated in a feedback circuit that operates independent of the photon source energy controls. The experimental program in parity violation at Jefferson Lab has already designed a position stabilization circuit that is able to keep the beam position steady to within 20µm over a 20m lever arm. A less sophisticated version of this circuit should be a part of the collimated photon source for Hall D.

The electron beam is dumped in the horizontal plane, as shown in Fig. 1. The horizontal bend offers several advantages over dumping the beam into the ground. The tagger magnet is easier to support if it sits in the horizontal position. It is also easier to mount and service the focal plane in this position. The dump itself is also more accessible in case it needs to be serviced. An above-ground dump also affords the possibility of running parasitic beam dump experiments that do not interfere with the operation of the experimental hall. It also allows for a possible future implementation of secondary meson beams in Hall D, which is the subject of the next section.

The primary design requirement for the electron beam dump is that it have a sufficiently high capacity to handle beams of the highest intensities foreseen for Hall D. A 250KW design would provide a a healthy margin for 12GeV operation and sufficient capacity to handle as much as 10µA in the planned 24GeV era. The present design calls for a 15^o bend in the horizontal plane from the axis along which the electron beam enters the tagger building to the direction it exits into the beam dump. The total 15^o bend is divided about equally between the tagger magnet and one or two dipoles. The dipoles were added as a cheaper alternative to enlarging the tagger magnet. It is considered that 15^o provides sufficient space for shielding that the experimental hall can be effectively isolated from the dump.

Fig. 7 A plan view of the tagging spectrometer from above, showing the path of the primary beam and the trajectory of post-bremsstrahlung electrons of various recoil momenta.

A plan view from above the tagger and focal plane is shown schematically in Fig. 7. The two primary requirements for the design of the focal plane hodoscope is that it have sufficient segmentation to provide the required photon energy resolution and that it be able to handle the high rates associated with coherent bremsstrahlung with collimation. Detector studies indicate that 0.1% r.m.s. photon energy resolution is required in the most demanding case, in order to make maximum use of the resolution of the detector to reconstruct incomplete events using the missing mass technique. Assuming that the energy of the incident electron beam is defined at the 0.1% level, a focal plane of non-overlapping counters each subtending a 25MeV bite of the total 6GeV momentum tagged at 12GeV electron beam energy provides the required tagged photon energy resolution. About 240 individual counters are required to completely instrument the tagger focal plane under these conditions. The detectors themselves can be little rectangular pieces of plastic scintillator no more than 2-3cm on a side and lined up with just enough overlap to prevent electrons from slipping between them without detection.

The counters subtending the upper 25% of the photon energy spectrum must be equipped with special bases and electronics to be capable of sustaining rates as high as 10MHz when running in collimated coherent mode. The part of the focal plane outside the coherent peak may as well be turned off for running in collimated mode because only the photons in the vicinity of the coherent peak are polarized. Given that one has a measurement of the energy of the photon from the tagger in any case, the primary reason for collimating the coherent beam is to enhance the polarization.