Running ParSA
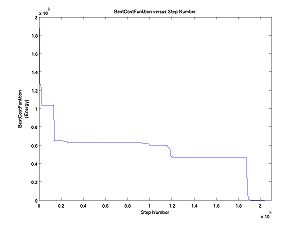
This page will serve as a progress report for the weekly work done on running the ParSA algorithm. Plots of cost function versus step number and the parameters used will be included for each completed run.
Information About ParSA and Technical Terms Used
The parSA (parallel simulated annealing) package from U. Paderborn, authors G. Kliewer and S. Tschoke) library is a general framework for solving large-scale optimization problems on a parallel computing platform. The package is written in c++ and uses the MPICH1 implementation of the standard MPI message passing interface library. Several terms are important for understanding the simulated annealing optimization procedure.
- problem - a solution space of parameters that should be searched to find the minimum of a function of the parameters, and a function whose value is to be optimized in a search of the solution space.
- energy - the function whose global minimum is being searched for.
- solution - the vector of parameters which are used to compute the energy.
- solution space - the set of all solutions that are consistent with the problem statement.
- neighborhood - a restricted region in solution space around a reference solution whose size is restricted to ensure that energy variations within a chain are reasonably continuous.
- neighborhood size - the number of distinct steps away from a given reference solution that exist within the solution space.
- step - a change in a solution vector that moves the solution within the neighborhood of the starting point, whose change in energy is accepted according to the Metropolis criterion.
- temperature - the criterion for accepting or rejecting a solution based on the Metropolis algorithm.
- Metropolis algorithm - an optimization algorithm that employs a random step generator and a binary choice at each step to accept or reject the step according to the probability max{1,exp(-ΔE/T)} where ΔE is the change in energy with the step and T is the temperature.
- chain - a sequence of steps that are connected to their neighbors by being nearby in solution space.
- subchain - a section of a chain that is generated at a fixed temperature, usually of length equal to neighborhood size.
- heating - initial phase of a run, during which a chain is generated, starting from a predefined initial solution, of sufficient length to measure the mean fluctuation scale of the energy within the neighborhood of the starting point. The starting temperature for the subsequent cooling cycle is computed from the average fluctuation scale measured on the heating chain so that some predefined criterion, such as the mean step acceptance ratio in the starting neighborhood, is satisfied.
- cooling - the second and final phase of a run, during which a solution chain is generated at a sequence of decreasing temperatures, starting from the initial temperature computed during the heating phase.
- schedule - a procedure for deciding at the end of each subchain how to adjust the temperature for the next subchain, or whether equilibrium has been reached.
- equilibrium - the condition, usually taken to define the end of a run, in which further decreases in temperature do not result in any significant decrease of the mean energy fluctuations within the local neighborhood.
- run - a single computing cycle of heating up followed by cooling down.
Questions and Answers About ParSA
Current Questions Being Addressed
We understand that parsa parallelizes the search by breaking up a subchain into n equal parts called "clusters". The question we are asking is, after each cluster is generated by each MPI slave process, how are the results accumulated by the main process?
- How is the main process taking advantage of the results for each cluster at the end of each subchain?
- Does each process generate one continuous chain, with only the temperature schedule reflecting information from other processes?
- Do each of them restart new subchains from a common starting point at each temperature transition?
- Does the results log written to disk by the head process contain all the information we need about the run?
- Do the individual files from each cluster (costfunction, temperature, bestcostfunktion) contain additional information that would be useful to keep?
Possible Answers to Questions
- Each cluster in a given subchain runs with the same temperature, which means that the temperature is distributed to all clusters each time it is recomputed at the end of the subchain.
- The length of each cluster varies from one subchain to the next, and one process to the next within a subchain. The scatter from one subchain to the next within a cluster (3300-4200) is larger than the scatter between subchains on a single cluster (50-100).
- The total length of the subchains is also variable, somewhere around 94000 but fluctuating by several hundred. Only process 0 has a consistent count, 4167 = nint(100000/24) every time. The neighborhood size was 100000 and cluster count was 24. Hypothesis: the head node has a fixed count of nint(neighborhood_size/cluster_count) and when it finishes it sends a message to the slaves to end their subchains and prepare to start a new subchain.
- Each process keeps a running tally of its best solution (with lowest energy) throughout the entire chain.
- At the end of each subchain, each cluster starts a new subchain segment at a common initial solution.
- The initial solution for each subchain is not the one with the best energy from any of the clusters, but is chosen from among the terminal solutions of the cluster subchains from the previous subchain according to the Metropolis algorithm (selected in the configuration file SA.cfg).
Job Runs
Here is where you can find each job we ran (as of Jan 21, 2008). Included under each subtitle is the configuration file that was used and the results of the completed run.
Week of 21 January 2008
The goal of the first run was to ensure that the MIR scheduler and solver would be able to successfully complete an entire run.
The parameters used for this run are as follows:
{
SA_Solver SA_MIRSolver
{
SA_Solver
{
datafilename data.ser
outputfilename parsaoutput
solutionfilename *
overwritesolution better
writefunction path
verbose on
verboselevel 10
StartSolution Init
}
SA_Scheduler SA_MIRScheduler
{
SA_Schedulerdouglas gregory
{
picturedirectory .douglas gregory
OptType MIN
thresholdvalue 0
initialtemperature -1.0
initaccratio 0.9
verboselevel 10
timelimit 100000
}
Alpha 0.5
Betta 2
endtemperature 0
Temperature_Reset 0
}
Betta_Runtime 1.1
Ebest 0
Epsilon 0.01
Maximum_RunLength RunFactor*GetLocalN()
Minimum_RunLength GetLocalN()
Samples 10
RunFactor 5
algorithm MIR
}
}
Running the MIR Solver/Scheduler
Questions about MIR
- Does the head node talk with the slave nodes?
- Do the result files keep track of the best solutions?
- How is the job divided amongst the nodes?
Answers to the MIR Questions
The head node does not exchange answers with the other nodes. The BestCostFunktion file only contains the head node's information.
justification: the minimum value of the head node's costfunction was the minimum found in the BCF file. While other nodes had found lower solutions. I do not have proof of the 22991 value, but I do have proof of solutions in the 20k's.
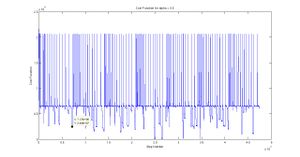
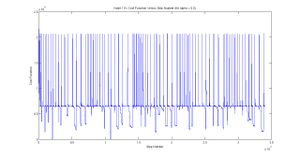
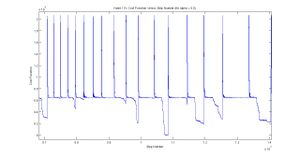
As far as I can tell now, the nodes all go through runs in unison. That is they each heat up cool down 10 times.
justification: A visual inspection of each of the nodes' cost functions shows less and less hill climbing as step number progresses (and temperature decreases). Since the number of this Cost Function density is periodic in step number, equalling about 7 in total (out of ten). The 7 is a result of the information from each node being taken before the end of the run. (NOTE: the claim about temperature versus the costfunction will need to be tested.)