Radphi Target Thickness

RadPhi TechNote
radphi-2000-501

Optimum Target Thickness for Radphi

Richard Jones
May 15, 2000

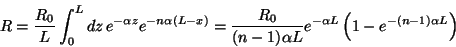
To first order in the cross sections, the rates in the Radphi detector are proportional to the product of beam rate times target thickness. At intensities high enough to hide cosmic rays this statement is true for both the signal and background contributions. At this level of approximation the sensitivity of the experiment is independent of target thickness, provided that one has enough beam current available. The 1999 summer run showed that the Hall B photon beamline was capable of generating enough beam current to saturate our rate capacity in the detector using a target 2.6cm long. This corresponds to about 6% of a photon absorption length in beryllium, the number that sets the scale for is size of the corrections to the leading-order approximation. From this point of view, changing the target thickness cannot improve things very much.

There are some experimental effects that are left out in this argument however.

Accidental coincidences with the tagger
Backgrounds in the detector from beam halo
Angular resolution in the calorimeter from target size
Conversions of final-state gammas in the target
Recoil proton energy loss in the target
Recoil proton energy loss in the target

Items 1 and 2 argue for lower beam current (i.e. longer targets) whereas 3-5 argue for shorter targets. The purpose of this note is to explore each of these effects and conclude with a recommended target length that achieves a compromise between them.

Tagger accidentals

The ratio of accidental to real coincidences in the tagger, under fixed trigger conditions, is proportional to the beam current. Under high-rate running conditions in summer 1999 our accidental rates were about 60% which means that 60% of all events with a true tag also come with a spurious hit in the tagger. This is not as bad as it sounds because it can be beat down somewhat offline by using the tagger TDC information to narrow the coincidence window. How well we can do at that depends on the time resolution of our BSD start, but I estimate that we might do a factor of 2 better offline after careful timing calibration. Having a third of our good events with a double-tag is not as bad as it sounds because our reconstruction does not rely on the tagger information; we reconstruct the final meson entirely from the calorimeter information. However the tagger information will almost certainly be useful offline to reject background from low-energy beam events. From these considerations I do not consider the tagging accidental rates to contribute a quantitative factor in the optimization of the target thickness. We just need to keep in mind the qualitative guiding principle of tagged photon experiments: all other things being equal, run at as low a photon intensity as you can afford. To see what we can afford we need to look at the remaining considerations.

Beam halo

Beam halo has been a real issue with Radphi during past test runs. During our first test run we found at one point that rates in the trigger counters were curiously insensitive to whether the target was present or not. We have come a long way since then, however. We have a helium bag, a lead shielding wall and an upstream charged-particle veto counter. Also significant for this run, we will have no CLAS target in the beam upstream. Experience during the 1999 summer test run showed us that the combination of all of this has reduced our rate contributions from beam halo to an insignificant level when the beam is properly tuned and steered. That might be a big WHEN. What we can say with some confidence is that we can expect beam conditions similar to what we had last year when the CLAS target was empty. Based on that experience, I take beam halo considerations to place an effective lower bound on the target thickness of 2.6cm, the value we had in 1999.

Photon angular resolution

We do not have a measurement of the vertex position. A kinematical fit of the event to known masses can be done to find the best vertex, but doing that we give up ability to suppress combinatoric background. Our best knowledge of the vertex position is knowing where the target is, which comes with an error given by the target length. So increasing the length of the target will contribute an additional uncertainty to the measured momenta of photons in the final state. From an earlier study of cluster centroid resolution in the E852 data sample I found an r.m.s. error in the transverse coordinates of about 1cm. To see how this gets combined with the target length to form an error on polar angle

, consider a worst case where the cluster is at the outer limits of reconstructable clusters in the lead glass 50cm from the beam axis. The target length does not contribute to the azimuthal angle resolution but it does add to the polar angle uncertainty. The total error in polar angle for such a high-angle forward cluster is shown in Fig. 1 versus target length. Beyond 5cm the contribution to the photon angular resolution from target length becomes appreciable.

Final-state gamma conversions

This consideration is important because it hits us where it hurts, in the statistics. All it takes is for one of the 5 final-state gammas from

decays to convert to e+e- inside the target and the event will be lost to the (offline) CPVeto. The r.m.s. of the photon beam is only 2.6mm at the Radphi target with 5.5GeV electron beam energy. For a target length of 2.6cm, a radius of 1.3cm and an effective cutoff angle of 25

for reconstructable showers in the lead glass, essentially all of the final-state photons from meson decays exit the target on its downstream surface. For longer targets an increasing fraction of the forward gammas exit the side of the target, but a good approximation to the conversion loss can be obtained by taking the z-distance from the interaction to the downstream end of the target as the path length to get out of the target. The following expression for the yield R of unconverted events normalized to the photoproduction yield R

takes into account attenuation of the primary beam inside the target as well.

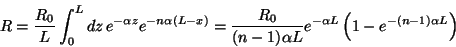(1)

where

is the photon absorption coefficient for the target, L is the length of the target and n is the number of forward gammas in the final state. For beryllium we have

=1/45cm. While the signal is being attenuated by absorption effects, I assume that the background rates remain constant, proportional to the beam intensity and the target thickness. This is because interactions in the target do not get rid of the background, they just redistribute it among a plethora of background modes. The function given by Eq. 1 is plotted in Fig. 2 vs. target length. This plot shows that the attenuation of final-state photons is a real concern when we consider using a longer target.

Recoil proton loss

Many of the recoil protons exit the target through the side. For these protons the length of the target has no effect. However for short targets some will exit the end, so there might be some additional premium for using short targets from this effect. To answer this question I need to look at Monte Carlo. I generated a set of

decays to a

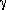with a few different target lengths and counted the number with exactly one pixel in the BSD and 5 clusters in the forward calorimeter that reconstruct to near the mass of the

. The results are shown in Fig. 3. The curve in the plot is that from Fig. 2 and the first data point has been arbitrarily normalized to fall on the curve. All of the other data points are normalized to the first one at 2.6cm target length. Agreement between the curve and the Monte Carlo data shows that the leading effect of target length on our yields is contained in Eq. 1 and that there are no large additional losses associated with recoil proton absorption in the target.

Conclusions

The above figures show that adding sections to our target comes at a cost in signal/background. Going from these results to a decision requires some discussion of the tradeoffs. In my own opinion, the advantages of improved tagging and lower beam halo backgrounds that are obtained by increasing the target thickness do not offset the cost in terms of signal/background. I would recommend keeping the same target thickness as we used last year.

We all know that the single most important factor in the success of this run is getting consistent performance out of the accelerator. The uncertainty in that term is probably on the order of a factor of . The one unspoken reason that might be motivating us to increase the target length is that we want to be as robust as possible in the presence of a poorly tuned beam or if there were somehow problems delivering 150nA to hall B. I am not very confident in our ability to anticipate the particular failure modes we will be facing, and suspect that the measures we take to be ready for them may end up hurting more than helping. As for what we are able to predict and control, I see no reason for either reducing or increasing our target length from what was used last year. However having extra target sections ready and available for installation in case that can get us up and running again in case of such a problem is sensible. If there are problems of this kind, the unhappy situation will probably be that we will have no difficulty getting the access time required for their installation.

This page is maintained by Richard Jones.