Hall D Internal Note
Beam Line Optics for Hall D
Report from meeting April 15, 1999
held at Jefferson Lab, Newport News, VA
Richard Jones
| Time: | 2:00pm on April 15, 1999 |
|---|---|
| Place: | Director's conference room, CEBAF Center |
| Present: | J. Benesch, R. Carlini, Y. Chao, D. Douglas, L. Harwood, R. Jones, V. Lebedev, C. Rode, E. Smith, D. Sober |
| Purpose: | to clarify the requirements for the transport of the CEBAF beam to the Hall D photon source and to discuss the next steps to be taken in the preparation of a design and cost estimate for the Hall D beam line. |
Background material from the Hall D Conceptual Design Report (Jan. 1999) had been distributed prior to the meeting. The meeting was opened by Lee Harwood, who presented the following list of items for discussion. These minutes are structured around this outline. Following that I have also included a few notes from the discussion that followed concerning the cost of the civil construction and its coupling to decisions regarding the beam line.
- Hall Geometry
- Detector type and footprint
- "Special" requirements
- polarimetry
- tagging
- energy measurement
- rastering
- dispersion matching (transverse coupling/decoupling, H-V exchanges, etc.)
- Dump geometry
- Beam Property Requirements
- Gross beam properties (including ranges/tolerances/stability)
- energy
- current
- Detailed phase space properties (including ranges/tolerances/stability)
- emittance / momentum spread
- spot size / bunch length
- position
- any average or peak current and/or timing structure
I. Hall Geometry
A. Detector type and footprint
This was discussed at another meeting held earlier the same day. Elton
summarized the present design, which envisions two surface buildings connected
by a tube. The detector building is 15m wide by 30m long by 13m high,
sufficient assuming that interior shielding does not require significant
real estate. The tagger building is 15m long, with transverse dimensions
yet to be decided, depending on whether the beam is dumped in the vertical or
horizontal plane. In the bending plane the dimension must allow at least 4m
from beam center to the wall on the side of the focal plane, and also leave
room for the post-tagger dipole(s). The post-tagger dipoles are included in
the design in order to achieve sufficient deflection
(15  ) of the electron beam
dump away from the photon beam line. The tube connecting the two
buildings will accommodate a helium-filled photon transport line and
some signal cables providing tagger information for the trigger. Just
outside the experimental hall where the tube enters there is a shielded
hut in which the photon collimation and sweep-magnet setup is located.
The mechanics of the spectrometer require that the photon beam line be
horizontal and a distance at least 2m above the floor of the experimental
hall.
) of the electron beam
dump away from the photon beam line. The tube connecting the two
buildings will accommodate a helium-filled photon transport line and
some signal cables providing tagger information for the trigger. Just
outside the experimental hall where the tube enters there is a shielded
hut in which the photon collimation and sweep-magnet setup is located.
The mechanics of the spectrometer require that the photon beam line be
horizontal and a distance at least 2m above the floor of the experimental
hall.
B. "Special" requirements
1. polarimetry
2. tagging
3. energy measurement
4. rastering
Richard Jones gave the following response. The Hall D conceptual design does not call for a polarimeter. In the process of coherent bremsstrahlung from a single lattice vector, the plane polarization of the coherent component of the photon beam is a simple function of the photon energy and the production angle of the photon. The same is true of the coherent flux. By measuring the photon flux profile in the tagger focal plane, the coherent fraction of the photon beam is measured precisely, together with its distribution in polar angle, and the azimuthally-averaged polarization can be extracted directly from that. The collimator geometry and electron beam optics are designed with azimuthal symmetry. There will be an electron beam stabilization system to maintain the alignment of the photon beam on the center of the collimator aperture. Systematics from imperfect alignment of the beam on the collimator can be checked by periodic runs with a very low beam current and tagging in coincidence with a counter directly in the beam behind the collimator.
Tagging places special requirements on the electron beam in three areas: energy spread, transverse emittance and dispersion. The discussion of the latter two came up again under item 5, and will be reported below. Monte Carlo studies have shown that missing mass resolution for certain final states is limited by the resolution of the tagger down to about 10MeV, or about 0.1% r.m.s. This is compatible with the electron beam momentum spread of 5MeV forecast (see Table III below) for CEBAF at 12GeV, but will require a careful analysis of the transverse emittance and dispersion of the beam in the bending plane in order to see that this resolution is obtained at the tagger focal plane.
The question of how accurately we need to know the electron beam energy in Hall D was then raised. Richard's initial reply was that the beam energy should be known to the 0.1% precision of the tagger. Elton pointed out that the absolute scale does not have to be known with this kind of precision, provided that it is stable and reproducible at this level. Lee explained that long term stability and reproducibility is much easier to assure at the 0.1% level than an absolute energy calibration, and stated that the absolute energy scale of the CEBAF beam is not currently known with 0.1% precision in the present halls. Richard agreed that it is stability and reproducibility over the long term that is required at the 0.1% level.
In the discussion on rastering, Lee explained the difference between two kinds of beam motion controls. A rastering system involves motion of the beam across the face of the target that is rapid on the scale of a second, such as what is used by high-current experiments to prevent the beam from drilling a hole through the target. If the motion is much slower, then it can be achieved by periodic adjustments to the beam steering elements, which is not called rastering. Richard explained that the beam motion foreseen for Hall D is for the purpose of spreading the radiation dose as uniformly as possible over the face of the crystal to prolong its useful lifetime. Since that lifetime is on the order of weeks at the highest currents, and since the beam spot is itself a sizeable fraction (10 - 20%) of the area of a typical crystal one might use, it was agreed that a rastering system is not needed.
In preliminary work on Hall D beam line design, the beam was specified to have zero dispersion at the radiator. Optimizing the tagging resolution may require adding some dispersion in order to compensate for dispersion inside the tagger magnet. The present design of the tagging magnet for Hall D is based upon the one currently used in Hall B, with a different curvature. Based upon what is known about dispersion properties of the the Hall B magnet, it should be possible to provide the necessary input to match the dispersion of the beam line to that of the tagger.
C. Dump geometry
Two options were discussed for the electron beam dump. Roger Carlini presented the option of dumping the beam vertically into the ground, and pointed out some advantages to this scheme in terms of shielding in the case of loss of power to the tagging magnet. If the tagging magnet were to trip off, the primary electron beam would sweep across the angular region between the dump and the photon beam line where it would remain until the safety controls shut it down. If the angular region between the dump and zero degrees were below the horizontal then this would simplify the safety requirements for this case.Richard Jones defended the horizontal dump described in the January draft of the design report based upon accessibility. Having an above-ground dump would make it more accessible for beam-dump experiments as well as for maintenance. At one of our workshops we heard a presentation from a Giovanni Bonvicini of Wayne State University proposing a measurement of the mass of the muon neutrino that that would need to accumulate a large number of low-energy pions from the beam dump. This low-budget experiment takes advantage of the c.w. nature of the CEBAF beam and the plans of hall D to run for long periods of time under fixed beam conditions. Such a source of low-energy pions would be a useful by-product of the experimental program, but it requires a horizontal dump. Concerning the safety issue raised by Roger, it was pointed out that the electron beam hits the return yoke of the tagging spectrometer as soon as it moves off its curved path into the dump. Thus the electron beam sees meters of iron before it can exit the tagger magnet over most of the angular range between the dump and zero degrees.
In the current design, the tagger magnet deflects the 12GeV beam by about
11 . An additional dipole
was added downstream of the tagger to bend the beam to
15
. An additional dipole
was added downstream of the tagger to bend the beam to
15 away from the beam axis
before it enters the dump. This additional bend was added to keep the
region forward of the dump away from the experimental hall and to help
shield the tagger building from back-wash from the dump. At 3µA and
12GeV the power being absorbed in the dump is 36KW. The present design
parameters being discussed at this meeting are for a maximum of 5µA
and 60KW in the beam dump.
away from the beam axis
before it enters the dump. This additional bend was added to keep the
region forward of the dump away from the experimental hall and to help
shield the tagger building from back-wash from the dump. At 3µA and
12GeV the power being absorbed in the dump is 36KW. The present design
parameters being discussed at this meeting are for a maximum of 5µA
and 60KW in the beam dump.
II. Beam Property Requirements
A. Gross beam properties (including ranges/tolerances/stability)
1. energy
2. current
The Hall D proposal is being based upon the choice of 12GeV for the endpoint energy. The Hall D collaboration believes that this is a good choice for the energy that optimizes its physics program within the limits set by the CEBAF accelerator and the laboratory's other programs. It was pointed out at the meeting earlier in the day that the final energy may be lie somewhere between 11 and 12GeV under the present accelerator upgrade plan. The collaboration did not discuss a figure for the minimum energy that would be acceptable to carry out its program, but instead affirmed its interest in obtaining the highest energy available from the accelerator. Nothing more than this was said on this point at the meeting being covered by these minutes. As stated above, stability and long-term reproducibility of the electron beam energy is required at the 0.1% level.
Also carried over into this meeting from the discussion earlier in the day
were the values shown in Table I for beam current and
power. The figure of 3µA for the electron beam current is based upon the
design goal of 10 photons/s in the
photon source configuration described in Table II.
Please note in particular
the power on the photon collimator. Parameters related to this quantity
are shown in the tables in bold type (flashing in the newer browsers).
In preparing these minutes, it was discovered that the figure of 100W
that I (Richard Jones) presented at the meeting is an order of magnitude
too large. Please note that nominal the nominal power on the collimator
can be reduced by an order of magnitude from what was discussed at the
meetings on April 15. I recommend values of 7W nominal, 10W
maximum for the total power contained in the photon beam prior to
collimation. The power figure after collimation remains unchanged.
Since these are meeting minutes, I report in Table I
the values that were discussed on April 15.
photons/s in the
photon source configuration described in Table II.
Please note in particular
the power on the photon collimator. Parameters related to this quantity
are shown in the tables in bold type (flashing in the newer browsers).
In preparing these minutes, it was discovered that the figure of 100W
that I (Richard Jones) presented at the meeting is an order of magnitude
too large. Please note that nominal the nominal power on the collimator
can be reduced by an order of magnitude from what was discussed at the
meetings on April 15. I recommend values of 7W nominal, 10W
maximum for the total power contained in the photon beam prior to
collimation. The power figure after collimation remains unchanged.
Since these are meeting minutes, I report in Table I
the values that were discussed on April 15.
Table I. Design parameters for electron beam in Hall D
| parameter | nominal value | design maximum |
|---|---|---|
| beam energy | 12 GeV | 12 GeV |
| beam current | 3 µA | 5 µA |
| electron dump power | 36 KW | 60 KW |
| photon collimator power | ||
| photon dump power | 1.0 W | 1.5 W |
Table II. Photon source configuration which forms the basis for the electron beam current requirements given in Table I.
| parameter | setting |
|---|---|
| electron beam energy | 12 GeV |
| electron beam current | 3 µA |
| energy of coherent peak | 9 GeV |
| f.w.h.m. of coherent peak | 600 MeV |
| total power in photon beam | |
| power in photon beam after collimator | 950 mW |
| flux within f.w.h.m. of coherent peak | 10 /s /s |
| maximum polarization in peak | 42 % |
| maximum tagging efficiency in peak | 50 % |
| diamond radiator thickness | 20 µm |
| r.m.s. mosaic spread of diamond crystal | 50 µr |
| horizontal angle of crystal from normal | -3.30 mr |
| vertical angle of crystal from normal | 100 mr |
| distance from radiator to collimator | 80 m |
| collimator diameter | 3.4 mm |
| electron beam emittance | 1.0×10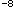 m·r m·r |
| r.m.s. beam spot size at focus | 500 µm |
B. Detailed phase space properties (including ranges/tolerances/stability)
1. emittance / momentum spread
2. spot size / bunch length
3. position
4. any average or peak current and/or timing structure
Richard Jones explained that the optics of the electron beam are what
controls the need for a long flight path between the radiator and the
collimator. Ideally the collimator has unit acceptance for bremsstrahlung
emitted at angles from zero up to some cutoff, and zero acceptance for
bremsstrahlung angles beyond the cutoff. How clean this separation can
be is controlled by the optics of the electron beam incident on the
radiator. The distribution of photons across the front face of the
collimator that have been emitted at exactly zero degrees from the
incident electron direction is called the "virtual spot size" in this
discussion. This is the shape the electron beam would have at the
collimator if the radiator were removed and the electron did not bend
in the magnetic field. This spot size must be much smaller than the
collimator diameter d in order for the acceptance at zero degrees
to be near unity. For a fixed angle of collimation
 = d / 2D and spot size, this places
a lower limit on radiator-collimator distance D. This is the
reason for the large value of D needed for the photon source.
= d / 2D and spot size, this places
a lower limit on radiator-collimator distance D. This is the
reason for the large value of D needed for the photon source.
In the optics design the spot size can be adjusted, subject to several
constraints. These following constraints were discussed at the meeting.
The fundamental constraint coming from the accelerator is the emittance
of the beam. Different definitions of emittance have appeared in several
places, which differ from each other by factors of 2 and
 .
For this and subsequent discussions we agreed upon a common definition
of the emittance.
.
For this and subsequent discussions we agreed upon a common definition
of the emittance.
The emittance of the electron beam is the product of the lengths of the semi-major and semi-minor axes of the 1The constraint from emittance is that reducing the virtual spot size requires that the angular divergence of the photon beam must increase proportionally. There are two new constraints that appear as a consequence of this.beam ellipse in phase space.
-
The spot size on the radiator must not be larger than of order 1mm r.m.s.
in order that the beam is contained inside a crystal of dimensions a few
mm on a side, and that the resolution in the tagger is not significantly
affected by beam size. Dispersion matching between the beam line and
the tagger magnet can be used to reduce the limiting tagging resolution from
the intrinsic energy spread of the electron beam, but it does not reduce
the limiting resolution from transverse beam size at the radiator. The
only way to reduce the latter limit is to reduce the spot size at the
radiator. This constraint effectively limits the virtual spot size to be
of order D·10
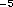 or larger,
assuming an emittance of 10
or larger,
assuming an emittance of 10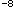 m·r.
m·r.
-
The kinematics of coherent bremsstrahlung relies a fine-tuning of the
angle between the incident electron and the planes of the crystal
radiator. As long as the divergence of the incident electron beam is
small compared to the intrinsic wiggles in the planes of the crystal itself
(known to crystallographers as mosaic spread) it is guaranteed not
to play a role in smearing out the coherent peak. Based upon the SLAC
experience we have taken in Table II
a figure of 50µr for the mosaic
spread of the radiator. If we take 20µr for the upper limit on the
allowed r.m.s. divergence of the electron beam, to keep it well below
the mosaic spread, this implies a lower bound of 500µr on the spot
size for an emittance of 10
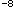 m·r, irrespective of D.
m·r, irrespective of D.
Solving these two constraints for D gives 50m. The present design stretches constraint 1 above by allowing the spot size on the radiator to expand to 1.6mm r.m.s. The second constraint has considerable safety built into it. Further study must be done to see how far it may be violated before serious degradation of the coherent effect is observed.
Given this input, Valery Lebedev provided the parameters in Table III as preliminary figures for the optics design. These values are the major outcome of the meeting. They form the starting point for a design of the transport beam line that connects the tagger building to the accelerator.
Table III. Starting values for the electron beam optics design from
| parameter | meaning | value |
|---|---|---|

|
horizontal emittance | 1.0×10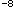 m·r m·r |

|
vertical emittance | 2.6×10 m·r m·r |
|
|
r.m.s. energy spread | 5.1 MeV |

|
horizontal r.m.s. divergence | 2.0×10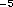 r r |

|
vertical r.m.s. divergence | 5.0×10 r r |
 * *
|
horizontal r.m.s. virtual spot size | 5.0×10 m m |
 * *
|
vertical r.m.s. virtual spot size | 5.0×10 m m |
 * *
|
horizontal beta function at virtual focus | 25 m |
 * *
|
vertical beta function at virtual focus | 100 m |

|
horizontal r.m.s. radiator spot size | 1.7 ×10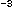 m m |

|
vertical r.m.s. radiator spot size | 6.4 ×10 m m |
The final discussion of the meeting was concerned with the cost of the beam line. It was agreed that the most important factor in making this estimate was deciding at what elevation the experimental hall would be constructed. Several of those present at this meeting were in favor of a below-ground solution. Clearly this would minimize the cost and complication of the beam line. A cost figure of $200K for the transport line was put forward for a configuration where the experimental hall would be located at the same level as the accelerator and located at the end of the north stub. A cost in excess of $2M, including the transport line, tunnel and optics elements, was put forward for a configuration with the experimental hall located at ground level. It was agreed that a conservative first-guess for the cost of the transport line could be obtained by looking back at the cost of the transport line to Hall B. The rule of thumb for costing beam lines is $20K per meter of beam line and $10K per meter of tunnel.
Elton Smith proposed that a preliminary cost estimate be made for three scenarios of the civil construction: deep trench (floor of hall at accelerator level), shallow trench (floor of hall 1-2 meters below grade) and ground level. It was agreed that discussions with those working on the civil construction design must be pursued further before a thorough design project is undertaken. The most important outcome of the meeting, from the point of view of the design report, is that all present agreed that the a transport line with the parameters shown in Table III can be designed, and that it would cost something less than $3M for any of the three civil scenarios.